Study 1

---

title: “[Data Structure] CS 스터디 1주차” excerpt: “시간복잡도, 공간복잡도, 링크드 리스트, 스택, 큐, 해시, 트리, 힙, 정렬”

categories:

• data-structure tags:
• [sort]

toc: true toc_sticky: true

sidebar: nav: “categories”

date: 2023-12-02 last_modified_at: 2023-12-24 —

깃허브 인터뷰 레포지토리에 있는 질문들을 가지고 매주 토론하는 스터디를 진행 중입니다.

시간복잡도, 공간복잡도

시간복잡도와 공간복잡도에 대해 설명해 주세요.

• 시간복잡도
  • 특정 알고리즘이 어떤 문제를 해결하는 데 걸리는 시간
• 공간복잡도
  • 작성한 프로그램이 얼마나 많은 공간(메모리)를 차지하느냐를 분석하는 방법

Big-O, Big-Theta, Big-Omega 에 대해 설명해 주세요.

• Big-O
  • 점근적 상한 표기 (증가율이 같거나 더 낮은 함수들의 집합)
  • ex) $2n^3 + 3n^2 - 25 \notin O(n^2)$
  • ex) $10n^2 + 3n - 25 \in O(n^2)$
• Big-Omega
  • 점근적 하한 표기 (증가율이 같거나 더 높은 함수들의 집합)
  • ex) $2n^3 + 3n^2 - 25 \in \Omega(n^2)$
  • ex) $10n^2 + 3n - 25 \in \Omega(n^2)$
• Big-Theta
  • Big-O와 Big-Omega의 표기가 같은 경우에 사용
  • ex) $2n^3 + 3n^2 - 25 \notin \theta(n^2)$
  • ex) $10n^2 + 3n - 25 \in \theta(n^2)$

다른 것을 사용하지 않고, Big-O를 사용하는 이유가 있을까요?

• 알고리즘 효율성을 상한선 기준으로 표기하기 때문
  • 알고리즘 효율성은 값이 클수록, 즉 그래프가 위를 향할수록 비효율적임

$O(1)$은 $O(N^2)$ 보다 무조건적으로 빠른가요?

• 입력의 수에 따라서 $O(N^2)$도 $O(1)$보다 빨라질 수 있다.
• 입력 크기가 작으면 $O(N^2)$의 알고리즘보다 $O(1)$의 알고리즘이 더 느릴 수 있다.

링크드 리스트

링크드 리스트에 대해 설명해 주세요.

• 링크드 리스트
  • 노드를 포인터로 연결하여 구현하는 리스트
  • 종류로는 단일 연결 리스트, 이중 연결 리스트, 원형 연결 리스트가 있음
    • 이중 연결 리스트
      • 단일 연결 리스트에 바로 전의 노드를 가리키는 previous 포인터를 추가한 연결 리스트
    • 원형 연결 리스트
      • 마지막 next 포인터가 연결 리스트의 노드를 가리키는 연결 리스트

일반 배열과, 링크드 리스트를 비교해 주세요.

• 일반 배열
  • 연속적인 메모리 공간상에 있으며, 인덱스를 이용한 접근이 $O(1)$로 빠름
  • 하지만 삽입과 삭제 연산의 경우, 배열의 데이터를 이동시켜야 하기 때문에 $O(N)$의 시간으로 수행됨
  • 메모리 할당: 컴파일
• 링크드 리스트
  • 연속적인 메모리 공간에 존재하지 않고, 포인터로 연결되어 있기 때문에 노드를 순차적으로 접근
  • 하지만 배열과 달리, 크기에 대한 제약이 없음
  • 또한 삽입, 삭제 연산이 $O(1)$의 시간으로 수행됨
  • 메모리 할당: 런타임

링크드 리스트를 사용해서 구현할 수 있는 다른 자료구조에 대해 설명해 주세요.

• 배열로 대부분의 자료구조는 구현 가능
• 대표적으로 스택과 큐가 있음

스택, 큐

스택과 큐에 대해서 설명해 주세요.

• 스택
  • Last In First Out을 하는 자료구조
  • 한 번 들어간 요소들은 나올 때 순서가 reverse 되어 나옴
• 큐
  • First In First Out을 하는 자료구조
  • 한 번 들어간 요소들은 나올 때 들어간 순서대로 나옴
  • add, remove, peek → 큐가 비어있을 때 null pointer 에러 발생
• 포인터로 알기

스택 2개로 큐를, 큐 2개로 스택을 만드는 방법과, 그 시간복잡도에 대해 설명해 주세요.

• 스택 2개로 큐 만들기
  • 삽입 연산
    • stack1로는 데이터 push
  • 삭제 연산
    • stack2로는 데이터 pop
    • 이때 stack2의 데이터가 비어있다면, stack1에서 stack2로 데이터 이동
  • 시간 복잡도
    1. stack2가 비어있을 때 pop
       • $O(N)$
    2. stack2가 비어있지 않을 때 pop, push
       • $O(1)$
• 큐 2개로 스택 만들기
  • 삽입 연산
    • queue2에 데이터 push
    • 만약 queue2 에 데이터가 있다면, queue1 기존 데이터를 push
  • 삭제 연산
    • queue2 에 데이터가 있는 경우
      • queue2 데이터 pop
    • queue2 에 데이터가 없는 경우
      • queue2 에 queue1 의 데이터가 하나 남을 때까지 이동 후 그 마지막 데이터를 pop
      • queue2 에 데이터가 하나 남을 때까지 데이터를 queue1 로 이동
  • 시간 복잡도
    • push, queue2 에 데이터가 있을 경우 pop
      • $O(1)$
    • queue2 에 데이터가 없을 경우 pop
      • $O(N)$

시간복잡도를 유지하면서, 배열로 스택과 큐를 구현할 수 있을까요?

• 스택
  • 어떤 상황에서든 가능
• 큐
  • 배열의 빈 공간을 미리 확보 후, 배열의 중간부터 큐의 head를 시작한다면 가능
  • 하지만 빈 공간보다 더 많은 수의 데이터가 삽입될 시, 더 많은 시간이 걸릴 가능성이 있음

Prefix, Infix, Postfix 에 대해 설명하고, 이를 스택을 활용해서 계산/하는 방법에 대해 설명해 주세요.

• Prefix (전위표기법)
  • +AB
  • 연산자를 먼저 표시하고, 연산에 필요한 피연산자를 나중에 표기하는 방법
  • 연산자를 만나면 push
  • 연속 두 개의 피연산자를 만날 시 pop
• Infix (중위표기법)
  • A+B
  • 연산자를 두 피연산자 사이에 표기하는 방법으로, 가장 일반적으로 사용되는 표현 방법
• Postfix (후위표기법)
  • AB+
  • 피연산자를 먼저 표기하고 연산자를 나중에 표기하는 방법
    • 컴파일러가 사용하는 것으로, 스택을 사용하는 예들 중 가장 빈번하게 등장함
  • 피연산자를 만나면 push
  • 연산자를 만나면 pop

Deque는 어떻게 구현할 수 있을까요?

• Deque 자료구조는 Stack과 Queue의 특성을 모두 갖는 자료구조
• 원형 큐를 확장하게 구현
• 나머지 연산들은 원형 큐와 같고, delete_rear() , add_front() 에서 rear와 front를 반대 방향으로 회전시키면 됨

front = (front - 1 + MAX_SIZE) / MAX_SIZE
rear = (rear - 1 + MAX_SIZE) / MAX_SIZE

해시

해시 자료구조에 대해 설명해 주세요.

• 해시
  • 여러 길이의 데이터를 효율적으로 관리하기 위해 해시 함수를 통해 일정한 길이의 값으로 매핑하는 것
  • 연결 리스트의 단점은 리스트에서 무언가를 찾고 싶을 때 무조건 모든 요소를 살펴봐야 한다는 점인데, 이러한 단점을 해결하여 데이터를 빠르게 추가하거나 제거하도록 한 데이터 구조

값이 주어졌을 때, 어떻게 하면 충돌이 최대한 적은 해시 함수를 설계할 수 있을까요?

• sha 256
• Division Method
  • 값을 버킷 사이즈로 나누어 나머지를 전체 버킷 사이즈에서 뺀 값으로 사용
  • 이 때 버킷 사이즈는 소수를 사용하고, 2의 제곱수와 먼 값을 사용하는 것이 좋음
• Digit Folding
  • 값이 문자열일 때 아스키 코드로 바꿔 합한 값을 사용
  • 이때 버킷 사이즈를 넘어갈 수 있기 때문에 Division Method를 함께 사용
• Multiplication Method
  • floor(K*A mod 1) * m 의 식을 사용
    • mod 는 나머지를 계산하는 연산자
  • A는 0과 1 사이의 실수, m은 2의 제곱수를 사용
• Universal Hashing
  • 여러 해시 함수를 무작위로 사용

해시값이 충돌했을 때, 어떤 방식으로 처리할 수 있을까요?

• 해시 충돌
  • 서로 다른 값을 가진 키가 일치하는 경우
• Chaining
  • 요소마다 연결 리스트를 만들어 수많은 데이터를 수용할 수 있게 하는 방법
  • 체인 해시는 가장 안정적이고 보편적으로 사용되는 자료 구조 중 하나
  • 체이닝을 하면 수용 가능한 요소 개수에 제한이 없어지고 크기 조정도 자주 할 필요가 없어짐
  • 적재율 λ는 항목의 개수를 가능한 체인 개수로 나눈 값
    • 체인 1개에 여러 항목을 넣을 수 있어 λ는 1보다 큰 수가 될 수 있음
      • 하지만 hashCode가 같은 숫자만 반환하여 하나의 체인이 너무 길어지면 결국 연결 리스트와 시간 복잡도가 같아지는 문제가 발생함
• Open Addressing
  • Open Addressing
    • 인덱스가 중복되었다면 다른 빈 인덱스를 찾아 저장하는 방법 1. 선형 조사법 (linear probing)
    • 채우려는 공간이 이미 차 있다면, 비어있는 칸을 찾을 때까지 다음 칸을 확인하는 방법
    • 비어있는 칸을 찾아 그 곳에 채운 후 위치가 바뀌었다는 사실을 알려야 함
      1. 2차식 조사법 (quadratic probing)
    • 다음 칸 대신 1부터 순서대로 제곱하여 더한 칸(12,22,…)(12,22,…)을 확인하는 방법
    • 테이블의 끝을 넘어간다면 % 연산을 해서 다시 테이블의 범위 안에 들어오게 함
      1. 이중 해싱 (double hashing)
    • hashCode 함수가 2개 있어 채우려는 공간이 이미 차 있다면 두 hashCode의 결과를 더한 값을 테이블 내의 위치가 되게 하는 방법
  • 이중 해싱은 아예 다른 해시 함수를 사용할 수 있기 때문에 데이터를 더 골고루 넣을 수 있음
    • 하지만 해시 함수가 2개 필요하다는 단점이 존재함
  • 선형 조사법과 2차식 조사법은 더하는 값(1, 2, 3, … 또는 1^2, 2^2, 3^2, …)에 규칙성이 있는 반면에
    • 이중 해싱은 두번째 해시 함수가 리턴하는 값이 임의적이기 때문에 배열의 더 다양한 위치에 값을 저장할 수 있음

본인이 사용하는 언어에서는, 어떤 방식으로 해시 충돌을 처리하나요?

• Java
  • jdk 7까지는 링크드 리스트를 사용한 sepearte chaining을 활용
  • jdk 8에서 링크드 리스트와 red black tree를 혼용한 separate chaining을 활용
    • 충돌을 한 key-value 쌍이 적을 때는 링크드 리스트로 작동
    • 충돌을 한 key-value 쌍이 특정 임계치에 도달하면 red black tree로 작동
    • 결론: 링크드 리스트는 탐색하는 데 시간 복잡도가 $O(N)$의 비용이 드는 반면에, red black tree는 $O(logN)$의 비용이 들기 때문에 jdk 8에서는 성능적으로 개선이 되었다고 볼 수 있음
• Double Hashing 의 장점과 단점에 대해서 설명하고, 단점을 어떻게 해결할 수 있을지 설명해 주세요.
  • Double Hashing
    • 개방 주소법 중 하나
    • 충돌이 발생한 버킷에 다른 버킷의 데이터를 저장하는 방식
    • 두 개의 해시 함수를 이용하여 다음 이동 위치를 결정하는 방식으로, 충돌 해결에 유용
  • 장점
    • 해시 테이블의 공간 사용을 최소화하고, 버킷들 사이의 균형을 맞추어 해시 충돌을 감소시킬 수 있음
  • 단점
    • 해시 함수의 선택이 중요하며, 잘못된 해시 함수 선택 시 일정한 패턴으로 충돌이 발생하여 클러스터링 현상이 발생할 수 있음
      • 클러스터
        • 해시 함수가 내뱉는 해시 값들이 저장 공간 한 쪽에 뭉치게 되는 경우, 저장 공간을 온전히 잘 활용해서 쓴다고 볼 수 없음
        • 예를 들어, 저장 공간이 0에서 100까지 있는데, 해시 함수가 30에서 50의 값 위주로 해싱한다면, 0~29과 51~100의 공간은 쓰이지 않게 낭비되게 됨
        • 이렇게 뭉쳐 있는 현상을 클러스터라고 하며, 클러스터 현상이 없을수록 좋은 해시 테이블이라 할 수 있음
    • 이를 해결하기 위해서는 두 개의 해시 함수를 서로 독립적으로 선택하고, 충돌이 발생한 경우에 대한 처리 방법을 세밀하게 조정하는 등의 조치를 취할 수 있음

트리

트리와 이진트리, 이진탐색트리에 대해 설명해 주세요.

• 트리
  • 노드와 간선으로 이루어져 있는 구조
  • 사이클이 없고 노드의 개수가 N 개라면 간선의 개수는 N-1 개를 가지는 구조
• 이진 트리
  • 각각의 노드가 자식 노드를 최대 2개 가지는 트리
• 이진 탐색 트리
  • 이진 트리 중 중복이 없고, 왼쪽 자식 노드는 루트보다 작고, 오른쪽 자식 노드는 루트보다 큰 값을 가지는 구조

그래프와 트리의 차이가 무엇인가요?

• 트리는 그래프의 일종임
• 하지만 트리는 그래프와 달리 방향성을 가지고, 사이클이 존재하지 않음

이진탐색트리에서 중위 탐색을 하게 되면, 그 결과는 어떤 의미를 가지나요?

• 오름차순의 형태가 나옴
• 이 이진 탐색 트리의 정렬된 순서를 읽을 수 있음

이진 탐색 트리의 주요 연산에 대한 시간복잡도를 설명하고, 왜 그런 시간복잡도가 도출되는지 설명해 주세요.

• 삽입
  • 삽입이 될 위치를 찾아야 되기 때문에 탐색과 동일하게 $O(logN)$
• 삭제
  • 삭제할 노드를 탐색하고, 만약 삭제된 자리를 대체하기 위한 노드를 찾아야 한다면 다시 탐색을 수행
  • 즉, 다른 연산들과 동일하게 $O(logN)$
• 탐색
  • 최악의 경우 트리의 높이만큼 탐색하기 때문에 $O(logN)$
  • 하지만 이 경우는 포화 트리일 경우이고, 편향 트리일 경우에는 $O(N)$
• 이진 탐색 트리의 한계점에 대해 설명해주세요.
  • 모든 연산이 트리의 높이에 의해 결정이 되기 때문에, 편향 트리일 경우 이진 탐색 트리의 장점을 살릴 수 없음
  • 이런 경우 때문에 AVL 트리 같은 개선된 트리가 나오게 됨
• 이진 탐색 트리의 값 삽입, 삭제 방법에 대해 설명하고, 어떤식으로 값을 삽입하면 편향이 발생할까요?
  • 삽입
    • 탐색하여 탐색을 실패한 자리에 값 삽입
  • 삭제
    • 삭제하려는 노드가 리프일 경우 그냥 삭제
    • 삭제하려는 노드가 하나의 서브 트리만 가지고 있는 경우, 삭제된 노드를 부모 노드에 연결
    • 삭제하려는 노드가 두 개의 서브 트리를 가질 경우, 왼쪽 서브 트리에서 가장 큰 자손을 올리거나 오른쪽 서브 트리에서 가장 작은 자손을 올림

힙

힙에 대해 설명해 주세요.

• 힙
  • 완전 이진 트리의 일종으로 반정렬 상태를 유지하여 최대 혹은 최소의 값을 빠르게 반환할 수 있는 자료구조
  • 주로 우선 순위 큐를 구현하기 위해 이용됨
  • 이진 탐색 트리의 단점을

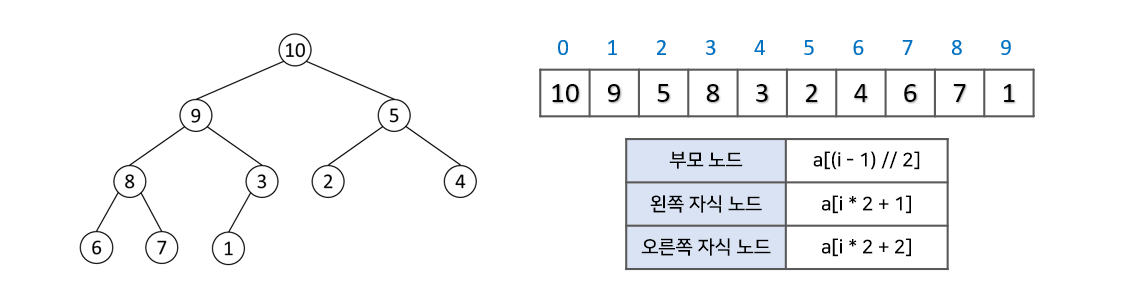
힙을 배열로 구현한다고 가정하면, 어떻게 값을 저장할 수 있을까요?

• 힙은 대체적으로 배열로 구현됨
  • 완전 이진 트리를 기본으로 하기 때문에 빈 공간이 없어 배열로 구현하기 용이함
• 아래 그림과 같이 루트 노드를 배열의 0번 index에 저장하고, 각 노드를 기점으로 왼쪽 자식 노드는 a[i * 2 + 1], 오른쪽 자식 노드는 a[i * 2 + 2]의 index에 저장됨
• 또한 특정 index의 노드에서 부모 노드는 a[(i - 1) // 2]로 찾을 수 있음

힙의 삽입, 삭제 방식에 대해 설명하고, 왜 이진탐색트리와 달리 편향이 발생하지 않는지 설명해 주세요.

• 삽입
  • 맨 마지막 자리에 요소를 삽입 후, 힙의 속성에 맞을 때까지 부모와 자식간의 교환을 함
• 삭제
  • 루트 노드와 맨 마지막 요소를 스왑한 후 마지막 요소를 반환
  • 그 후 힙의 속성에 맞을 때까지 부모와 자식간의 교환을 함
• 편향이 발생하지 않는 이유
  • 이진 탐색 트리에서 편향이 발생하려면 완전 정렬된 상태로 삽입이 이루어져야 함
  • 하지만 이때 힙은 최대 혹은 최소 요소를 루트 노드로 하는 완전 이진 트리를 유지하도록 삽입 및 삭제를 하기 때문에 편향이 발생하지 않음

힙 정렬의 시간복잡도는 어떻게 되나요? Stable 한가요?

• 힙 정렬의 시간 복잡도는 힙을 구성하고 나서 삭제 연산을 반복하면 되므로 $O(NlogN)$임
• Unstable함

BBST

BBST (Balanced Binary Search Tree) 와, 그 종류에 대해 설명해 주세요.

• 이진 탐색 트리의 단점을 보완한 트리
• 편향 트리가 발생하지 않도록 삽입 혹은 삭제를 할 때 높이의 균형을 유지하는 트리
• 그 종류로는 AVL, red black tree, B tree, B+ tree 등이 있음

Red Black Tree는 어떻게 균형을 유지할 수 있을까요?

• 조건
  1. 모든 노드는 빨강 혹은 검정
  2. 루트 노드는 검정
  3. 모든 리프는 검정
  4. 빨강 노드의 자식은 검정
  5. 모든 리프 노드에서 black depth는 동일
     • 리프 노드에서 루트 노드까지 가는 경로에서 만나는 검정 노드의 개수가 같음
• 삽입
• 삭제

Red Black Tree의 주요 성질 4가지에 대해 설명해 주세요.

1. 루트 노드는 검정
2. 모든 리프는 검정
3. 빨강 노드의 자식은 검정
4. 모든 리프 노드에서 black depth는 동일

2-3-4 Tree, AVL Tree 등의 다른 BBST가 있음에도, 왜 Red Black Tree가 많이 사용될까요?

• Red Black Tree
  • 삽입, 삭제 작업 시 균형을 맞추기 위한 작업 횟수가 적음
  • 각 노드당 색을 표현하는 데 단 1 bit의 저장 공간만 필요
  • 언제 회전에 의해 균형을 잡아야 하는지가 쉽게 판별됨
  • 이진 탐색 트리의 함수를 거의 그대로 사용함
• AVL Tree
  • 조회 시 더 빠른 성능을 자랑함
  • 노드에 색이 없음
  • 빠르지만 재균형 잡는 시간이 듦
  • 프로그래밍과 디버깅이 어려움
  • Balance Factor를 이용해 밸런스를 유지
    • 모든 노드의 BF가 -1, 0, 1 중 하나여야 함
  • BF(K) = K의 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이
• 2-3-4 Tree
  • 2 노드, 3 노드, 4 노드가 있는 균형 탐색 트리
    • n 노드란 n - 1개의 키와 n 개의 자식을 가지고 있다는 의미
  • 한 노드의 한 키의 왼쪽 부분 트리에 있는 모든 키 값은 그 키 값보다 작고, 오른쪽 부분 트리에 있는 모든 키 값은 그 키 값보다 커야 함
  • 모든 리프 노드의 높이는 동일
  • 삽입 연산은 4 노드에서 스플릿 연산이 이루어짐
  • 노드 구조가 복잡함
  • 삽입 삭제 코드가 복잡함

정렬

정렬 알고리즘에 대해 설명해 주세요.

• 정렬 알고리즘
  • 어떠한 자료구조를 정렬하는 방법
  • Quick Sort, Merge Sort, Radix Sort, Counting Sort, Bubble Sort, Insertion Sort, Selection Sort 등이 있음

Quick Sort와 Merge Sort를 비교해 주세요.

• Quick Sort
  • pivot을 기준으로 나눠 정렬하는 기법
• Merge Sort
  • 자료구조를 분할 후에 합치면서 정렬하는 방법
• Merge Sort는 최악, 평균, 최선일 경우 모든 $O(nlogN)$의 시간이 소요되는 반면, Quick Sort는 역순으로 정렬되어 있을 시 pivot의 효과를 볼 수 없기 때문에 최악의 경우 $O(n^2)$의 시간이 소요됨

Quick Sort에서 O(N^2)이 걸리는 예시를 들고, 이를 개선할 수 있는 방법에 대해 설명해 주세요.

• 오름차순 혹은 내림차순으로 정렬되어 파티션이 나뉘지 않는 경우
• 이를 개선하기 위해서는 중간값과 맨앞값을 서로 스왑해주면 어느 정도의 개선이 가능

Stable Sort가 무엇이고, 어떤 정렬 알고리즘이 Stable 한지 설명해 주세요.

• Stable Sort
  • 중복된 값이 있을 시 이 순서가 변경되지 않는 정렬을 의미
  • Insertion Sort, Merge Sort, Bubble Sort, Counting Sort가 Stable 함

Merge Sort를 재귀를 사용하지 않고 구현할 수 있을까요?

• 큐를 이용하여 구현할 수 있음

Radix Sort에 대해 설명해 주세요.

• Radix Sort
  • 자릿수를 이용해 정렬을 하는 정렬 기법
  • 0~9에 해당하는 버킷을 만들고, 낮은 자릿수부터 진행하며, 순서대로 해당하는 자릿수의 버킷에 요소를 저장하고 정렬시키는 과정을 반복하여 정렬하는 기법
• 시간 복잡도
  • $O(dN)$
    • d : 자릿수

Bubble, Selection, Insertion Sort의 속도를 비교해 주세요.

• 시간 복잡도는 모두 $O(N^2)$

값이 거의 정렬되어 있거나, 아예 정렬되어 있다면, 위 세 알고리즘의 성능 비교 결과는 달라질까요?

• Selection Sort는 정렬되어 있을 시 비교 연산만 하기 때문에 $O(N^2)$가 아니라 $O(N)$의 시간 복잡도를 가짐

본인이 사용하고 있는 언어에선, 어떤 정렬 알고리즘을 사용하여 정렬 함수를 제공하고 있을까요?

• Java
  • Arrays.sort()
    • Dual-Pivot Quick Sort 사용
    • 일반적인 Quick Sort와는 다르게 pivot을 2개를 두고 3개의 구간을 만들어 Quick Sort를 진행함
    • 랜덤 데이터에 대해서 평균적으로 Quick Sort보다 좋은 성능을 냄
  • Collections.sort()
    • Tim Sort 사용
      • Tim Sort는 Insertion Sort와 Merge Sort를 결합하여 만든 정렬
      • Java 7부터 Tim Sort를 채택하여 사용하고 있음
  • Arrays를 정렬했을 때와 Collections를 정렬했을 때 사용하는 알고리즘이 다른 이유
    • 참조 지역성의 원리 때문
      • 참조 지역성의 원리
        • 동일한 값 또는 해당 값의 근처에 있는 스터리지 위치가 자주 액세스되는 특성
    • 참조 지역성의 원리는 CPU의 캐싱 전략에 영향을 미침
      • 즉, CPU가 데이터를 액세스하며 해당 데이터만이 아니라 인접한 메모리에 있는 데이터 또한 캐시 메모리에 함께 올려둠

정렬해야 하는 데이터는 50G 인데, 메모리가 4G라면, 어떤 방식으로 정렬을 진행할 수 있을까요?

1. 4G만큼 데이터를 메모리에 읽어 일반적인 정렬 알고리즘을 이용해 정렬함
2. 그러면 13개의 파일이 생김
3. 280MB씩 각 파일의 앞부분을 읽어옴 (남은 280MB는 출력을 위한 버퍼)
4. 280MB씩 Merge를 수행하고 출력 버퍼에 작성. 출력 버퍼가 차면 파일에 쓰고 출력 버퍼를 비움. 입력 버퍼가 비워지면 다음 용량만큼 읽음