[Data Structure] CS 스터디 14주차

깃허브 인터뷰 레포지토리

링크드 리스트에 대해 설명해 주세요

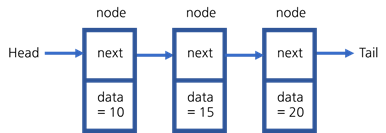
포인터를 사용하여 여러 개의 노드를 연결하는 자료 구조를 연결 리스트라고 합니다.

• 단일 연결 리스트
  • 각 노드가 다음 노드만을 가리키는 포인터를 가짐
  • 한 방향으로만 순회 가능
• 이중 연결 리스트
  • 각 노드가 이전 노드와 다음 노드를 가리키는 두 개의 포인터를 가짐
  • 양방향 순회 가능
• 원형 연결 리스트
  • 마지막 노드가 첫 번째 노드를 가리킴
  • 단일 또는 이중 연결 리스트 모두 원형으로 구성 가능

일반 배열과, 링크드 리스트를 비교해 주세요

특성	배열	링크드 리스트
메모리 할당	연속된 공간, 고정 크기	분산된 공간, 동적 크기
접근 시간	$O(1)$	$O(N)$
삽입/삭제	$O(N)$	$O(1)$
메모리 효율	높음	포인터로 인해 낮음

링크드 리스트를 사용해서 구현할 수 있는 다른 자료구조에 대해 설명해 주세요

스택(Stack)

• 링크드 리스트의 한쪽 끝에서만 삽입과 삭제가 이루어지도록 구현
• push 연산은 리스트의 앞쪽에 노드를 추가
• pop 연산은 첫 번째 노드를 제거
• LIFO(Last In First Out) 구조 구현 가능

큐(Queue)

• 한쪽 끝에서는 삽입, 다른 쪽 끝에서는 삭제가 이루어지도록 구현
• enqueue 연산은 리스트의 끝에 노드를 추가
• dequeue 연산은 리스트의 앞에서 노드를 제거
• FIFO(First In First Out) 구조 구현 가능

해시 테이블(Hash Table)

• 체이닝
  • 해시 테이블이란 키-값 쌍을 저장하는 자료구조
    • 서로 다른 키가 같은 해시 값(인덱스)을 가지는 충돌 문제가 발생할 수 있음
  • 체이닝은 이러한 충돌을 해결하는 방법 중 하나

• 체이닝 방식의 충돌 해결을 위해 링크드 리스트 사용
• 각 버킷에 링크드 리스트를 둬서 같은 해시값을 가진 요소들을 저장
• 충돌이 발생할 경우 해당 버킷의 링크드 리스트에 새로운 노드 추가

그래프(Graph)

• 인접 리스트(Adjacency List)
  • 그래프를 표현하는 자료구조
  • 각 정점(vertex)마다 해당 정점과 인접한 정점들을 리스트로 저장
  • 예를 들어 정점 1이 정점 2, 3, 4와 연결되어 있다면 다음과 같이 표현됨

• 인접 리스트 방식으로 그래프 구현 가능
  • 각 정점마다 링크드 리스트를 사용하여 인접한 정점들을 저장
• 메모리를 효율적으로 사용할 수 있음
• 특히 희소 그래프(Sparse Graph) 표현에 적합

트리(Tree)

• 각 노드가 여러 개의 자식 노드를 가리키는 포인터를 포함하도록 구현
• 이진 트리 등 다양한 트리 구조 구현 가능
• 파일 시스템의 디렉토리 구조 등을 표현하는데 활용

트리와 이진트리, 이진탐색트리에 대해 설명해 주세요

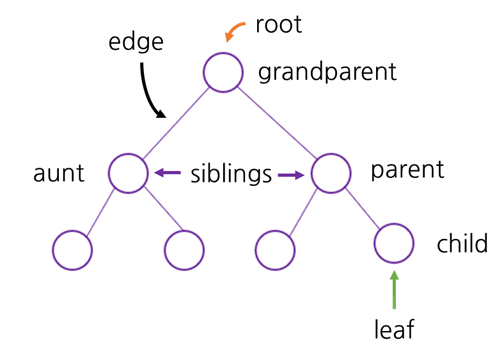
• 트리
  • 가계도처럼 노드를 나무 형태로 연결한 구조
  • 트리에 있는 각각의 요소는 노드
  • 모든 노드는 0개 이상의 자식 노드를 가질 수 있음
  • 각 노드는 하나의 부모 노드만을 가짐
• 이진 트리
  • 모든 노드가 최대 두 개의 자식 노드를 가질 수 있는 트리 구조
  • 종류
    • 완전 이진 트리: 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨은 왼쪽부터 채워진 이진 트리
    • 포화 이진 트리: 모든 레벨이 완전히 채워진 이진 트리
    • 균형 이진 트리: 왼쪽과 오른쪽 서브트리의 높이 차이가 1 이하인 이진 트리
• 이진 탐색 트리
  • 왼쪽 서브트리의 모든 노드는 현재 노드보다 작은 값을 가짐
  • 오른쪽 서브트리의 모든 노드는 현재 노드보다 큰 값을 가짐
  • 중복된 값을 허용하지 않음

그래프와 트리의 차이가 무엇인가요?

특성	그래프	트리
방향성	방향 그래프(Directed) 또는 무방향 그래프(Undirected) 모두 가능	부모 노드에서 자식 노드로의 단방향 계층 구조
순환성	순환(Cycle) 가능. 시작 정점으로 돌아오는 경로 존재 가능	순환 불가. 어떤 노드도 자신의 조상이 될 수 없음
루트	특별한 시작점 없음	단 하나의 루트 노드가 존재하며, 모든 노드는 정확히 하나의 부모를 가짐
경로	두 정점 사이에 여러 경로 존재 가능	임의의 두 노드 사이에 유일한 경로만 존재
연결성	연결 또는 비연결 모두 가능	항상 연결되어 있음. 모든 노드는 루트에서 도달 가능
간선 수	제한 없음	$n$개의 노드에 대해 정확히 $(n-1)$개의 간선
리프 노드	개념 없음	자식이 없는 노드를 리프 노드라 하며, 최소 2개 이상 존재

이진탐색트리에서 중위 탐색을 하게 되면, 그 결과는 어떤 의미를 가지나요?

이진 탐색 트리에서 중위(inorder) 탐색을 수행하면 노드들의 키 값을 오름차순으로 얻을 수 있습니다.

• 이진 탐색 트리는 모든 노드에 대해 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 큰 값을 가집니다.
• 중위 탐색은 왼쪽 서브 트리 → 현재 노드 → 오른쪽 서브 트리 순으로 방문합니다.
• 이러한 특성들이 결합되어 자연스럽게 오름차순 정렬된 결과를 얻게 됩니다.

활용성

• 정렬된 데이터가 필요한 경우 효율적으로 사용
• 특정 범위의 값을 검색할 때 유용
• 데이터의 순서 관계를 파악할 때 활용

예시

     5
   /   \
  3     7
 / \   / \
2   4 6   8

중위 탐색 결과: 2, 3, 4, 5, 6, 7, 8 (오름차순 정렬)

이진탐색트리의 주요 연산에 대한 시간복잡도를 설명하고, 왜 그런 시간복잡도가 도출되는지 설명해 주세요

기본 시간복잡도

모든 기본 연산(검색, 삽입, 삭제)의 시간복잡도는 트리의 높이$(h)$에 비례하여 $O(h)$입니다.

시간복잡도가 이렇게 도출되는 이유

• 검색 연산: $O(h)$
  • 각 노드에서 비교 후 왼쪽 또는 오른쪽으로 이동
  • 한 번의 비교로 탐색 범위가 절반으로 감소
  • 트리의 높이만큼만 비교하면 됨
• 삽입 연산: $O(h)$
  • 삽입할 위치를 찾기 위해 검색과 동일한 과정 필요
  • 위치를 찾은 후 실제 삽입은 $O(1)$
  • 총 시간복잡도는 $O(h) + O(1) = O(h)$
  • 결과적으로 검색과 동일한 시간복잡도
• 삭제 연산: $O(h)$
  • 삭제할 노드를 찾는 과정이 필요: $O(h)$
  • 노드 삭제 후 트리 재구성 필요: $O(1)$
  • 자식이 2개인 경우 successor 노드 찾기: $O(h)$
    • successor 노드: 이진 탐색 트리에서 특정 노드의 다음 노드를 의미
  • 총 시간복잡도는 $O(h) + O(h) + O(1) = O(h)$
  • 전체적으로 검색과 동일한 시간복잡도

상황별 시간복잡도

• 최선의 경우: $O(log N)$
  • 트리가 균형잡힌 경우
  • 각 레벨마다 노드 수가 2배씩 증가
  • $n$개의 노드를 가진 트리의 높이는 $log N$이 됨
  • 매 연산마다 탐색 범위가 절반으로 감소
• 최악의 경우: $O(N)$
  • 트리가 한쪽으로 치우친 경우(편향 트리)
  • 연결 리스트처럼 직선 형태가 됨
  • 높이가 $n$이 되어 모든 노드를 순회해야 할 수 있음

이진탐색트리의 한계점에 대해 설명해주세요

트리의 불균형 문제

• 편향 트리 발생
  • 데이터가 정렬된 순서로 삽입될 경우 한쪽으로 치우친 편향 트리가 됨
  • 예를 들어 1, 2, 3, 4, 5 순서로 삽입하면 오른쪽으로만 자식이 생성됨
  • 결과적으로 링크드 리스트와 유사한 형태가 됨

    1
     \
      2
       \
        3
         \
          4
           \
            5

• 성능 저하
  • 균형이 무너진 경우 시간복잡도가 $O(log N)$에서 $O(N)$으로 저하됨
  • 탐색, 삽입, 삭제 모든 연산의 효율성이 떨어짐
  • 트리의 높이가 커질수록 성능이 악화됨

해결 방안

• 자가 균형 트리 사용
  • AVL 트리: 노드의 삽입/삭제 시 자동으로 균형을 맞춤
  • 레드-블랙 트리: 색상 규칙을 통해 균형을 유지
  • B-트리: 다진 트리 구조로 균형을 유지

이진탐색트리의 값 삽입, 삭제 방법에 대해 설명하고, 어떤식으로 값을 삽입하면 편향이 발생할까요?

값 삽입 방법

1. 루트 노드부터 시작하여 비교를 통해 적절한 위치 찾기
2. 삽입할 값이 현재 노드보다 작으면 왼쪽으로 이동
3. 삽입할 값이 현재 노드보다 크면 오른쪽으로 이동
4. 빈 위치를 찾으면 그 자리에 새로운 노드를 삽입

값 삭제 방법

• 자식이 없는 경우(리프 노드)
  1. 해당 노드를 단순히 제거
• 자식이 하나인 경우
  1. 삭제할 노드의 부모와 자식을 직접 연결
  2. 삭제할 노드를 제거
• 자식이 둘인 경우
  1. 오른쪽 서브 트리의 최솟값 또는 왼쪽 서브 트리의 최댓값 찾기
  2. 찾은 값을 삭제할 노드 위치로 복사
  3. 최솟값/최댓값 노드를 삭제

// 자식이 둘인 경우
       10
      /  \
     5    15
    / \   / \
   3   7 12  17

// 1. 오른쪽 서브트리의 최솟값(12)을 찾음
// 2. 10을 12로 교체
// 3. 원래 12가 있던 노드(10)를 삭제

// 결과
       12
      /  \
     5    15
    / \     \
   3   7     17

편향 발생 케이스

1. 정렬된 순서로 삽입
   • 오름차순으로 삽입 (1,2,3,4,5…)
   • 내림차순으로 삽입 (5,4,3,2,1…)
2. 특정 패턴을 가진 데이터 삽입
   • 일정한 간격의 숫자 삽입

// 1. 오름차순 삽입
 1 -> 2 -> 3 -> 4 -> 5

결과:
1
 \
  2
   \
    3
     \
      4
       \
        5

// 2. 일정한 간격의 숫자 삽입
// 10 -> 20 -> 30 -> 40 -> 50

결과:
10
 \
  20
   \
    30
     \
      40
       \
        50

편향 예방법

• 데이터를 랜덤하게 삽입
• 자가 균형 트리 사용
• 주기적인 재균형화 수행

이진탐색트리와 동일한 로직을 사용하면, 삼진탐색트리도 정의할 수 있을까요? 안 된다면, 그 이유에 대해 설명해 주세요

Binary Search Tree vs Ternary Search Tree

삼진 탐색 트리는 이진 탐색 트리와 동일한 로직으로 구현할 수 없습니다.

데이터 저장 방식의 차이

• 이진 탐색 트리의 데이터 저장
  • 각 노드가 하나의 완전한 키 값을 저장
  • 모든 노드가 동일한 타입의 데이터를 저장
  • 단순 대소 비교로 처리
• 삼진 탐색 트리의 데이터 저장
  • 각 노드가 문자(character) 단위로 데이터를 저장
  • 문자열이 여러 노드에 걸쳐 분산되어 저장됨
  • 문자 단위의 비교가 필요

노드 구조의 차이

• 이진 탐색 트리의 노드 구조
  • 왼쪽, 오른쪽 두 개의 자식 노드만 존재
  • 단순 대소 관계로 나뉨
• 삼진 탐색 트리의 노드 구조
  • 왼쪽(작은 값), 중간(같은 값), 오른쪽(큰 값) 세 개의 포인터를 가짐
  • equal 포인터는 문자열의 다음 문자로 이동하는 특별한 역할 수행

• equal 포인터는 현재 문자와 일치하는 경우 문자열의 다음 문자로 이어지는 경로를 나타냄

// 문자열 집합 {CAB, CBA, CDA, CEA, CFA}에서의 탐색 과정

                C
                |
                | (equal)
                ↓
    A -------> B -------> D -------> E -------> F
    |          |          |          |          |
    | (equal)  | (equal)  | (equal)  | (equal)  | (equal)
    ↓          ↓          ↓          ↓          ↓
    B          A          A          A          A  
    CAB        CBA        CDA        CEA        CFA

1. 루트 노드 ‘C’에서 시작하여 찾고자 하는 문자열의 첫 글자와 비교
2. 현재 문자와 비교하여 세 가지 방향으로 이동
   • 찾는 문자가 더 작으면 왼쪽으로
   • 찾는 문자가 같으면 가운데 eqaul 포인터로 이동하여 다음 문자 검사
   • 찾는 문자가 더 크면 오른쪽으로

• 예를 들어 “CEA”를 찾는 경우
  1. C(루트) → equal 포인터 → 두 번째 레벨
  2. A부터 시작하여 E를 찾을 때까지 오른쪽으로 이동
  3. E에서 equal 포인터를 따라 마지막 문자 A로 이동

탐색 과정의 차이

• 이진 탐색 트리의 탐색
  • 각 노드에서 키 값 전체를 한 번에 비교
  • 비교 결과에 따라 왼쪽 또는 오른쪽으로만 이동
  • 한 번의 비교로 탐색 방향 결정
• 삼진 탐색 트리의 탐색
  • 각 노드에서 한 문자씩 순차적으로 비교
  • 비교 결과에 따라 세 가지 방향으로 이동
    • 현재 문자보다 작으면 left로 이동
    • 현재 문자와 같으면 equal 포인터로 이동하여 다음 문자 검사
    • 현재 문자보다 크면 right로 이동
  • 문자열의 끝까지 매칭이 성공해야 탐색 완료

이러한 근본적인 차이들로 인해 서로 다른 구현 방식이 필요합니다.