[Data Structure] Sort (정렬)

Published: 2022-05-20
Updated: 2023-12-04

정렬

앞으로 정렬을 하는 데 쓰이는 알고리즘을 다뤄볼 것입니다. 그리고 이 알고리즘을 다양한 방법으로 비교할 것입니다.

이 수업에서는 숫자들을 순서대로 정렬하는 경우만 다룰 예정입니다. 문자열, object 등을 대상으로 정렬할 수도 있지만 숫자만 사용할 것입니다.

out-of-place 정렬과 in-place 정렬

out-of-place 정렬은 모든 데이터를 자료 구조의 복사본에 옮긴 후 순서대로 배열하여 정렬하는 방법입니다. 그리고 in-place 정렬은 자료 구조를 그대로 두고 그 안에서 요소들의 위치를 바꾸어 정렬하는 방법입니다.

안정 정렬과 불안정 정렬

안정 정렬은 중복된 숫자가 원래 순서를 유지한 상태로 정렬하는 방법입니다. 반대로, 불안정 정렬은 중복된 숫자의 순서를 보장할 수 없습니다.

시간 복잡도

모든 정렬 알고리즘에 대해 최악의 경우, 평균적인 경우, 최선의 경우의 복잡도를 알아볼 것입니다. 최악의 경우는 정렬 전에 큰 수에서 작은 수로 있는 경우, 최선의 경우는 이미 정렬되어 있는 경우입니다. 평균적인 경우는 완전히 임의의 순서로 되어 있는 리스트를 정렬하는 경우를 의미합니다.

선택 정렬

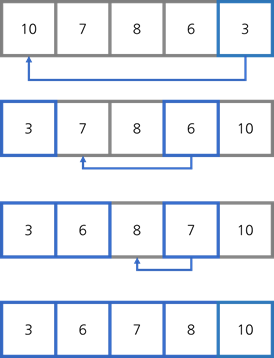
선택 정렬(select sort)은 순서대로 리스트의 가장 작은 수를 찾고 그 수를 확정되지 않은 부분의 가장 앞 자리에 놓는 방법입니다. 리스트 안에서 순서만 바꿔주기 때문에 in-place 정렬입니다.

첫 번째 칸에서는 n-1번 대소 비교를 하고 그 이후로 n-2번, n-3번, … , 1번 비교하기 때문에 이들을 모두 합하면, 복잡도는 $O(n^2)$이 됩니다. 리스트가 이미 정렬되어 있다고 하더라도 대소 비교를 해야 하므로 최선, 최악, 평균의 경우 모두 $O(n^2)$이 됩니다.

삽입 정렬

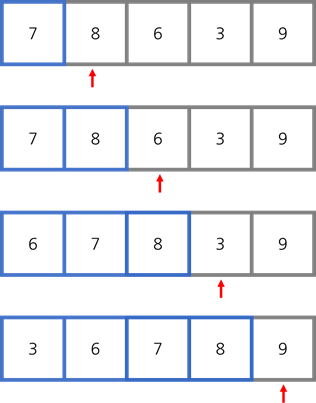
삽입 정렬(Insertion sort)은 요소를 하나씩 꺼내서 그 요소 앞에 있는 다른 요소들과 모두 비교하는 방법입니다. 리스트 안에서 순서만 바꿔주기 때문에 in-place 정렬입니다.

최악의 경우, 두 번째 칸에서는 1번 대소 비교를 하고 그 이후로 2번, 3번, … , n-1번 비교하기 때문에 이들을 모두 합하면, 복잡도는 $O(n^2)$이 됩니다. 평균적인 경우에도 복잡도는 $O(n^2)$입니다. 하지만 이미 순서에 맞게 정렬되어 있다면 각각 1번씩 n-1번 비교하면 되므로 복잡도는 $O(n)$이 됩니다.

삽입 정렬은 잘 정렬된 딕셔너리나 데이터베이스에 정렬된 몇 개의 요소를 추가할 때 자주 사용합니다. 이 경우에 복잡도는 O(n)에 가까워집니다. 이미 정렬된 부분은 다시 정렬할 필요가 없기 때문입니다.

삽입 정렬 (코드)

for 반복문을 사용하여 삽입 정렬을 구현합니다.

// 요소를 선택하여 v에 저장
for (int i=1; i < array.length; i++) {
	int j;
	v = array[i];
	for (int j=i-1; j >= 0; i--) {
		// v가 바로 전의 요소보다 크거나 같으면 break
		if (array[j] <= v)
			break;
		// v가 바로 전의 요소보다 작으면 위치를 바꿔줌
		array[ j+1 ] = array[ j ];
	}
	array[ j+1 ] = v;
}

셀 정렬

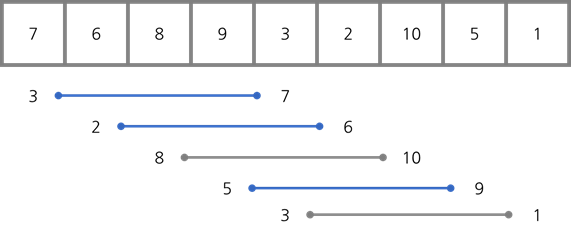
셀 정렬(Shell sort)은 일정한 너비만큼 떨어진 요소를 가져와서 그 둘을 대소비교한 후 바꾸는 방법입니다. 처음에는 큰 간격으로 시작해서 더 적은 간격으로 정렬을 하고 간격의 크기가 1이 되면 삽입 정렬을 합니다. 즉, 셀 정렬은 작은 값을 가진 요소는 오른쪽에서 왼쪽으로 옮기고 큰 값을 가진 요소는 왼쪽에서 오른쪽으로 옮기는 알고리즘입니다.

셀 정렬은 중복된 숫자의 순서가 보장되지 않는 불안정 정렬입니다. 그리고 리스트 안에서 순서만 바꿔주기 때문에 in-place 정렬입니다.

최악의 경우, 삽입 정렬과 같아지므로 복잡도는 $O(n^2)$입니다. 셀 정렬의 평균적인 시간 복잡도는 얼마의 간격을 사용했는지에 따라 달라집니다.

합병 정렬

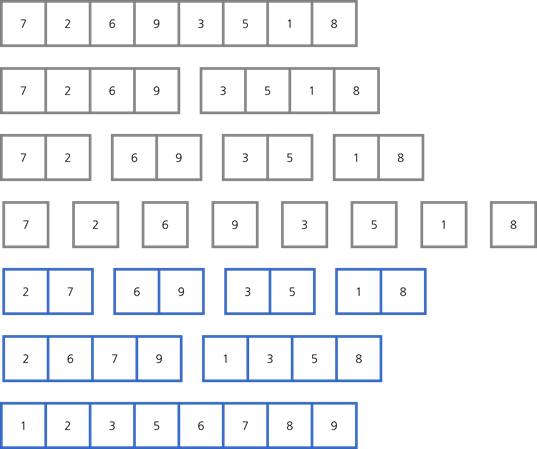
합병 정렬(Merge sort)은 요소가 하나만 남을 때까지 리스트를 나눠준 후, 나눴던 리스트를 대소 관계에 맞게 다시 합치는 방법입니다.

합병 정렬은 중복된 숫자의 순서가 유지되는 안정 정렬입니다. 그리고 리스트를 나눠 다른 공간에 저장해야 하기 때문에 out-of-place 정렬입니다.

리스트를 나눌 때마다 필요한 대소 비교의 횟수가 줄어들어 평균적인 시간 복잡도는 $O(nlogn)$이 됩니다.

합병 정렬 (코드)

합병 정렬을 코드로 구현하면 다음과 같습니다.

int[] array, temp;
public mergeSort(int[] array) {
	this.array = array;
	// 빈 배열을 만들어 데이터가 정렬되면 이를 저장
	temp = new int[array.length];
	split(0, array.length - 1);
}
// 리스트가 1개 남을 때까지 나눕니다.
public void split(int low, int high) {
	if (low == high) return;
	int mid = (high + low) / 2;
	split (low, mid)
	split (mid + 1, high)
	merge (low, mid, high)
}
// 대소 비교 후 순서에 맞게 열거합니다.
public void merge(int low, int mid, int high) {
	int i=low, j=mid+1, tempposn = low;
	// 나눈 리스트의 대소 비교와 정렬
	while (i <= mid && j <= high) {
		if (array [i] <= array [j])
			temp[tempposn++] = array[i++];
		else
			temp[tempposn++] = array[j++];
	}
	// // i가 mid로 가고 j가 high로 갈 때까지 반복
	while (i <= mid) temp[tempposn++] = array[i++];
	while (j <= high) temp[tempposn++] = array[j++];
	// 원래 배열에 다시 복사
	for (tempposn = low; tempposn <= high; tempposn++)
		array[tempposn] = temp[tempposn];
}

퀵 정렬

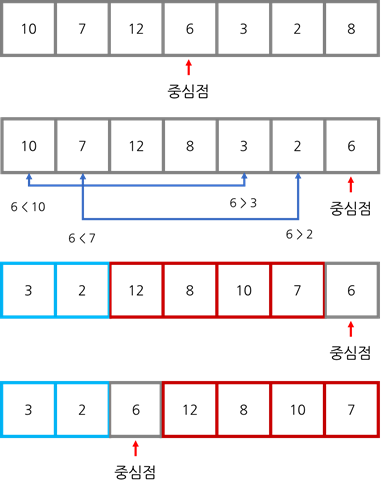
퀵 정렬(Quicksort)은 중심점(Pivot Point)을 임의로 고른 후 이 중심점보다 작은 수를 한 쪽으로 분류하고 큰 수들은 다른 쪽으로 분류하여 정렬하는 방법입니다.

퀵 정렬 알고리즘은 Python, C, C++의 표준 라이브러리나 Java의 sort 메소드에서 사용하는 정렬 알고리즘입니다. 그리고 모든 종류의 변수에 대해 사용 가능합니다.

중심점의 왼쪽에 있는 숫자들은 오른쪽에 있는 숫자들과 비교할 필요가 없습니다. 리스트를 분리하여 따로 비교하므로, 평균적인 경우에 시간 복잡도는 $O(nlogn)$입니다.

퀵 정렬은 다음과 같은 순서로 이뤄집니다.

중심점을 선택합니다. 주로 리스트의 중간에 있는 숫자 혹은 마지막에 있는 숫자를 선택합니다.
마지막 요소와 중심점의 위치를 바꿔 중심점을 리스트의 가장 끝으로 보냅니다.
2개의 카운터를 사용하여 리스트의 처음부터 탐색합니다. 첫 번째 카운터에는 중심점보다 큰 숫자의 위치를 저장하고 두 번째 카운터에는 현재 탐색하고 있는 위치를 저장합니다.
탐색하며 중심점보다 작은 숫자를 발견하면 첫 번째 카운터의 숫자 위치와 바꿔줍니다.
3, 4 과정을 반복하면 중심점보다 큰 수와 중심점보다 작은 수가 나눠지게 됩니다.
다시 중심점을 선택하여 2~5 과정을 반복하면 리스트가 정렬됩니다.

퀵 정렬 (최악의 케이스)

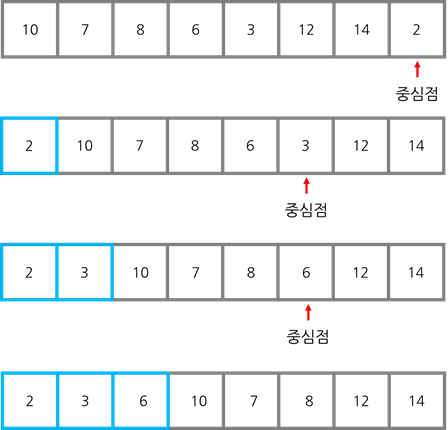
퀵 정렬에서는 전체 데이터를 계속해서 반으로 줄여나가기 때문에 평균적인 상황에서는 $O(nlogn)$의 시간 복잡도를 갖습니다. 하지만 최악의 경우, 계속해서 최소인 지점을 중심점으로 잡는다면 시간 복잡도는 $O(n^2)$까지도 늘어날 수 있습다. (모든 숫자가 중심점보다 커서 대소비교만 하고 분류가 되지 않는 경우입니다.)

퀵 정렬 (코드)

모든 종류의 변수에 대해 사용 가능한 퀵 정렬을 코드로 구현하면 다음과 같습니다.

public class QuickSort <E> {
	E[] array;
	// 제너릭 생성자
	public E[] sort(E[] array) {
		this.array = array;
		quicksort(0, array.length - 1);
		return array;
	}
	// 위치를 바꿔주는 함수
	public void swap(int from, int to) {
		E tmp = array[from];
		array[from] = array[to];
		array[to] = tmp;
	}
	// 퀵 정렬
	public void quicksort(int from, int to) {
		// 정렬 종료
		if (from >= to) return;
		// 중심점(Pivot Point)으로 배열의 마지막에 있는 숫자를 선택합니다.
		E value = array[to];
		// 중심점보다 큰 값을 가리키는 카운터
		int counter = from;
		// 중심점의 바로 앞까지 탐색
		for (int i=from; i < to; i++) {
			// 중심점보다 작은 값을 발견하면 중심점보다 큰 값과 위치를 바꿉니다.
			if (((Comparable<E>) array[i].compareTo(value) <= 0) {
				swap(i, counter);
				counter++;
			}
		}
		// 중심점이 중간에 오게 합니다.
		swap(counter, to);
		// 배열의 왼쪽과 오른쪽을 정렬합니다. 카운터의 위치는 맞는 자리이므로 더 이상 옮길 필요가 없습니다.
		quicksort(from, counter - 1);
		quicksort(counter + 1, to);

}

기수 정렬

기수 정렬(Radix)은 우편번호, 자릿수 등의 기준을 만들어 기준에 따라 숫자를 분류하여 정렬하는 방법입니다.

예를 들어, 4자리 숫자를 일의 자리의 숫자, 십의 자리의 숫자, 백의 자리의 숫자, 천의 자리의 숫자에 따라 분류하여 정렬할 수 있습니다. 이럴 경우 시간 복잡도는 4n이 됩니다.

이론적으로 이 방법은 $n$ 의 복잡도를 갖는 빠른 정렬 방법입니다. 하지만 실제로는 숫자를 복사하는 과정이 너무 많아 수행 속도가 느립니다. 그래서 컴퓨터에서는 사용하기 어렵고 일상 생활에서 우편물을 정렬할 때와 같이 기계적으로 정렬할 때 많이 쓰입니다.

정렬 요약

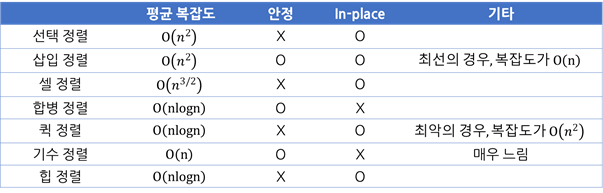
지금까지 선택 정렬, 삽입 정렬, 셀 정렬, 합병 정렬, 퀵 정렬, 기수 정렬, 힙 정렬을 공부하였습니다. 각각의 시간 복잡도와 특징을 위 표와 같이 정리할 수 있습니다.

Reference

BoostCourse

Sully