[Data Structure] Linked List (연결 리스트)

연결 리스트

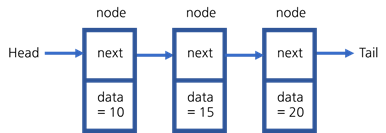
포인터를 사용하여 여러 개의 노드를 연결하는 자료 구조를 연결 리스트라고 합니다.

연결 리스트의 기본 구성 요소는 노드입니다. 노드에는 두 가지 정보가 들어있습니다. 첫 번째는 인접한 노드를 가리키는 next라는 이름의 포인터, 두 번째는 우리가 노드에 넣는 데이터를 가리키는 포인터입니다. (노드 D의 경우, 다음에 아무것도 없기 때문에 null을 가리킵니다)

이 리스트는 head라는 이름의 포인터에서 시작합니다. Head는 리스트의 첫 번째 노드를 가리킵니다. 힙에서는 이 연결 리스트의 head만 알고 있기 때문에, head.next 혹은 head.data 등으로 노드의 내용을 찾습니다. 하지만 연결 리스트의 길이가 매우 길 경우, 계속 head 뒤에 next를 붙일 수는 없습니다. 그래서 임시 포인터를 사용하여 탐색하는 방법을 사용합니다.

다음 수업에서는 이러한 연결 리스트를 어떻게 만들고 제거하는지 공부하도록 하겠습니다.

배열과의 차이점

배열 또한 순서대로 여러 데이터를 저장할 때 사용한다는 공통점이 있습니다. 하지만 배열은 필요한 요소보다 너무 크게 만들거나 너무 작게 만들어 배열의 크기를 조정해야 한다는 문제점이 있습니다.

배열과 다르게, 연결 리스트는 항상 맞는 크기로 만들어지도록 설계되어 있습니다. 그래서 순차적인 데이터나 많은 양의 데이터가 있을 때 자주 사용됩니다.

노드와 크기

public class LinkedList <E> implements ListI<E>{
	// 노드 정의
	class Node<E>{
		E data;
		Node<E> next;
		public Node(E obj){
			data=obj;
			next=null;
		}
	}
	private Node<E> head;
	// 노드 개수를 세는 변수
	private int currentSize;
	// 기본 연결리스트
	public LinkedList(){
		head=null;
		currentsize=null;
	}
}

위 코드는 연결 리스트의 내부 클래스에서 노드를 정의한 내용입니다. 노드는 next라는 포인터와 data를 가집니다.

data의 자료형은 E입니다. E는 정해지지 않은 자료형이고 이렇게 구현한 연결 리스트를 사용하면 그때 지정하겠다는 의미입니다. 그리고 next의 타입은 Node입니다. 다른 노드를 가리키는 포인터이기 때문입니다.

생성자까지 추가하여 코드를 적으면 노드 객체가 완성됩니다. 생성자에서는 객체를 data에 저장하고 next는 우선 null로 지정합니다. 이 노드 객체는 내부 클래스이기 때문에 연결 리스트가 아닌 다른 곳에서 접근할 수 없습니다. 외부에서 접근하기 위해 노드 객체를 만들 때와 같이 private 변수 head를 만듭니다.

노드의 개수를 세는 효율적인 방법

노드의 개수를 직접 세는 방법보다 int 타입인 변수 currentSize를 만들어 노드의 개수를 세는 방법이 더 효율적입니다.

노드의 개수를 직접 셀 경우, 요소가 $n$개면 $n$번 세야 합니다. 따라서, 하나씩 세는 것의 시간 복잡도는 $θ(n)$입니다. 하지만 currentSize라는 변수를 만들어놓고 리스트에 요소를 추가할 때마다 currentSize의 값을 늘려 놓으면, 리스트의 크기를 바로 알 수 있습니다. 이럴 경우, 시간 복잡도는 정확히 1입니다.

경계 조건

Boundary Conditions

• Empty data structure

• Single element in the data structure

• Adding / removing beginning of data structure

• Adding / removing end of the data structure

• Working in the middle

어떤 자료 구조든 아래의 경계 조건에서 문제가 생기진 않을지 생각해봐야 합니다.

1. 자료 구조가 비어있는 경우

2. 자료 구조에 단 하나의 요소가 들어있을 때

3. 자료 구조의 첫 번째 요소를 제거하거나 추가할 때

4. 자료 구조의 마지막 요소를 제거하거나 추가할 때

5. 자료 구조의 중간 부분을 처리할 때

addFirst 메서드

새로운 node를 연결 리스트의 앞부분에 추가하는 방법은 다음과 같습니다.

1. 새로운 node를 만든다.
2. 새로운 node의 next가 현재 head를 가리키도록 한다.
3. head 포인터가 다시 새로운 노드를 가리키도록 한다.

이 과정을 코드로 작성하면 다음과 같습니다.

public void addFirst(E obj){
	Node<E> node = new Node<E>(obj); // 1
	node.next = head; // 2
	head = node; // 3
}

위 코드는 5가지 경계 조건에 대하여 생각하였을 때에도 문제가 없습니다. 그리고 새로운 요소를 추가하기 위해 뒷부분을 살펴볼 필요가 없기 때문에 시간 복잡도는 1입니다.

addLast 메서드

addLast 메소드에서는 연결 리스트의 마지막을 가리키는 임시 포인터를 사용합니다. 연결 리스트의 요소를 확인하려면 무조건 head에서 시작해야 하는데, 연결 리스트의 마지막까지 도달하는 데 next를 너무 많이 사용해야 하기 때문입니다.

그리고 연결 리스트의 마지막 노드는 유일하게 next 포인터가 null을 가리키기 때문에, 아래 코드와 같이 addLast 메소드를 작성할 수 있습니다.

public void addLast(E obj){
	Node<E> tmp = head;
	while(tmp.next != null)
		tmp=tmp.next
	tmp.next=node;
}

문제 1. 경계 조건

head가 비어있는 경우에는 tmp가 null이 되고, tmp.next를 찾지 못하는 NullPointerException 에러가 발생합니다. 이 문제를 해결하기 위해 리스트 맨 뒤에 추가하려 하는데 리스트가 비어있다면, addFirst 메소드처럼 노드를 추가합니다. 이 내용을 추가한 코드는 아래와 같습니다.

public void addLast(E obj){
	Node<E> node = new Node<E>(obj);
	if (head == null){ // head가 비어있는 경우
		head=node;
		currentsize++;
		return;
	}
	Node<E> tmp = head;
	while(tmp.next != null)
		tmp=tmp.next
	tmp.next=node;
	currentsize++;
}

문제 2. 시간 복잡도

연결 리스트의 마지막 노드를 찾을 때 리스트의 맨 앞부터 시작해서 마지막 요소까지 살펴보면 시간 복잡도는 $O(n)$ 입니다. 하지만 tail 포인터를 사용하면 이 시간 복잡도를 $O(1)$ 로 만들 수 있습니다. 리스트의 마지막을 가리키는 tail 포인터를 head, currentSize와 같은 전역 변수로 설정하고, 아래와 같이 tail 포인터를 추가하면 됩니다.

public void addLast(E obj){
	Node<E> node = new Node<E>(obj);
	if (head == null){
		head=node;
		tail=node; // head 포인터뿐만 아니라 tail 포인터도 바꿔줘야 합니다.
		currentsize++;
		return;
	}
	tail.next=node;
	tail = node;
	currentsize++;
}

removeFirst 메소드

보통의 경우, head=head.next를 하면 head가 다음 노드를 가리키게 되고 첫 번째 노드가 제거됩니다. 하지만 다음과 같은 경계 조건에서 에러가 발생하므로 코드를 추가해야 합니다.

경계 조건 1. 자료 구조가 비어있는 경우

head가 null을 가리키는 경우입니다. 이 때, head가 head.next를 가리키게 하면 NullPointerException 에러가 발생하게 됩니다. 그래서 이 상황에서는 아무것도 하지 않고 null을 반환하면 됩니다.

경계 조건 2. 자료 구조에 단 하나의 요소가 들어있을 때

head 포인터, tail 포인터 모두 null을 가리키게 해야 합니다.

코드를 작성하면 다음과 같습니다.

public E removefirst(){
	// 경계 조건 1
	if (head == null)
		return null;
	E tmp = head.data;
	// 경계 조건 2
	if (head == tail) // head.next == null, currentSize == 1도 가능
		head = null;
		tail = null;
	// 그 외의 경우
	else
		head = head.next;
	currentSize--;
	return tmp;
}

removeLast 메소드

마지막 노드를 마지막에서 2번째 노드로 옮겨 연결리스트의 마지막 노드를 제거합니다. 단일 연결 리스트이기 때문에 2번째 노드를 찾으려면 head에서부터 시작해야 합니다.

임시 포인터 current와 previous를 활용하여 마지막에서 2번째 노드를 찾을 수 있습니다. current는 현재 위치를 가리키는 포인터이고 previous는 이전 위치를 가리키는 포인터입니다. current 포인터가 tail과 같으면 previous 포인터는 마지막에서 2번째 노드를 가리키게 됩니다.

이번에도 경계 조건에서 에러가 발생하므로 코드를 추가해야 합니다. 자료 구조가 비어있는 경우와 자료 구조에 단 하나의 요소가 들어있을 때 removeFirst에서와 똑같이 예외 처리를 해주면 됩니다.

코드를 작성하면 다음과 같습니다.

public E removeLast(){
	// 자료 구조가 비어있는 경우
	if (head == null)
		return null;
	// 자료 구조에 단 하나의 요소가 들어있을 때
	if (head == tail)
		return removeFirst();
	// 그 외의 경우
	// 임시 포인터 current, previous를 활용하여 마지막 노드를 제거합니다.
	Node<E> current = head,
	Node<E> previous = null;
	while (current != tail) {
		previous = current;
		current = current.next;
	}
	previous.next = null;
	tail = previous;
	currentSize--;
	return current.data;
}

find

Comparable 인터페이스를 사용하여 노드를 찾습니다.

public boolean contains(E obj){
	Node<E> current = null;
	while(current != null) {
		if (((Comparable<E>) obj).compareTo(current.data)==null) // Comparable 인터페이스
			return true;
		current = current.next;
	}
	return false;
}

remove

1. Comparable 인터페이스를 사용하여 제거하고 싶은 요소의 위치를 찾습니다.

2. 바로 앞 노드의 next 포인터가 다음 노드를 가리키게 만들어 가운데 노드를 제거합니다. previous, current의 2가지 포인터를 사용하여 각각 바로 앞의 노드와 제거하고자 하는 노드를 가리키게 합니다.

노드가 1개만 있는 경우, 첫 번째 노드를 제거하는 경우에는 removeFirst 메소드를 사용합니다. 그리고 마지막 요소를 제거하는 경우에는 removeLast 메소드를 사용합니다.

public E remove(E obj){
	Node<E> current = head;
	Node<E> previous = null;
	while(current != null) {
		if (((Comparable<E>) obj).compareTo(current.data)==null) { // 1. find
			if (current==head) // 노드가 1개 or 첫 번째 노드 제거
				return removeFirst();
			if (current==tail) // 마지막 노드 제거
				return removeLast();
			currentsize--;
			previous.next=current.next; // 2. remove
			return current.data;
			}
		previous = current;
		current = current.next;
	}
	return null;
}

peek 메서드

peek 메소드는 하나의 요소를 살펴보기 위해 쓰는 메소드입니다. 추가, 제거하는 것이 아니라 그 요소의 내용을 읽는 함수입니다.

peekFirst는 아래와 같이 구현할 수 있습니다. 리스트가 비어있으면 NullPointerException 에러가 발생하기 때문에 따로 처리해줍니다.

public E peekFirst(){
	if (head == null)
		return null;
	return head.data;
}

같은 방식으로 하여, peekLast는 아래와 같이 구현할 수 있습니다. 임시 포인터를 활용하여 시간 복잡도가 $O(n)$ 인 peekLast 함수를 만들 수도 있습니다.

public E peekLast(){
	if (tail == null)
		return null;
	return tail.data;
}

연결리스트 테스트

연결리스트를 직접 만들어 지금까지 배운 메소드를 테스트할 수 있습니다. ListI 인터페이스를 구현한 LinkedList를 테스트하는 방법은 다음과 같습니다.

public class Tester {
	public static void main (String[] args){
		static ListI<Integer> List = new LinkedList <Integer>();
		int n=10;
		// 연결 리스트를 만듭니다.
		for(int i=0; i<n; i++)
			list.addFirst(i); // addLast도 가능
		// 연결 리스트를 제거합니다.
		for(int i=n-1; i>=0; i--)
			int x=list.removeFirst(); // removeLast도 가능
}

반복자

배열의 각각의 원소를 출력할 때, 다음과 같이 코드를 작성합니다.

int arr[] = {1,2,3,4,5};
for (int i=0; i<arr.length; i++){
	system.out.println(arr[i]);
}

혹은, 다음과 같이 나타낼 수 있습니다.

int arr[] = {1,2,3,4,5};
for (int x:arr){
	system.out.println(x);
}

하지만 객체에서 두 번째 방식으로 반복문이 동작하도록 하기 위해서는 Iterator 인터페이스를 구현해야 합니다. Iterator 인터페이스를 구현하는 코드는 다음과 같습니다.

public Iterator<E> iterator(){
	return new IteratorHelper();
}

public class LinkedList<E> implements ListI<E>{
	class IteratorHelper implement Iterator<E>{
		Node<E> index;
		public IteratorHelper(){
			index=head;
		}
		public boolean hasNext(){
			return (index != null)
		}
		public E next(){
			if (!hasNext())
				throw new NoSuchElementException();
			E val = index.data;
			index = index.next;
			return val;
		}
	}
}

이중 연결 리스트

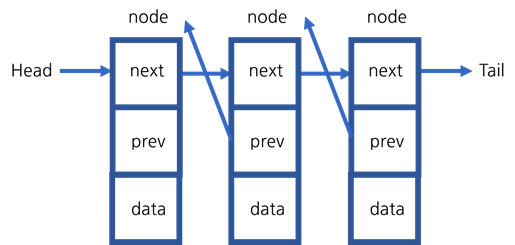
이중 연결 리스트는 단일 연결 리스트에 바로 전의 노드를 가리키는 previous 포인터를 추가한 연결 리스트입니다.

removeLast 메소드를 사용할 때, 단일 연결 리스트는 tail 포인터가 있더라도 $O(n)$ 의 시간 복잡도로 모든 노드를 한 번씩 거쳐야 한다는 단점이 있었습니다. 하지만 이중 연결 리스트는 tail 포인터가 가리키는 노드에서 previous 포인터가 가리키는 노드를 찾으면 되기 때문에 시간 복잡도가 $O(1)$ 이 됩니다.

이중 연결 리스트의 단점은 previous 포인터가 추가되기 때문에 노드를 추가하는 과정이 더 복잡해진다는 것입니다.

원형 연결 리스트

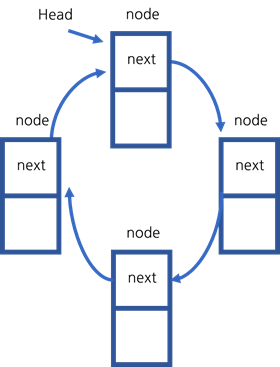
원형 연결 리스트는 마지막 next 포인터가 연결 리스트의 노드를 가리키는 연결 리스트입니다.

원형 연결 리스트의 마지막 next 포인터가 head를 가리키는지 확인하는 방법은 다음과 같습니다.

• head에서 시작하여 t==null이 될 때까지 반복한다면, 시간복잡도는 $O(n)$ 입니다.
• tail 포인터를 사용할 경우, 시간복잡도는 $O(1)$ 입니다.

마지막 next 포인터가 임의의 노드를 가리킨다면 확인하는 방법은 다음과 같습니다.

• tail에서 시작하여 tail 포인터가 다시 나타나는지 확인합니다. 시간복잡도는 $O(n)$ 입니다.
• 임시 포인터 2개를 사용하여 시작점을 잡고 currentSize만큼 떨어진 노드까지 확인한 후 시작점을 다음으로 옮겨 같은 노드가 나타날 때까지 반복합니다. 시간복잡도는 $O(n^2)$ 입니다.

Source

• BoostCourse