[Data Structure] Heap & Tree (힙 & 트리)
트리
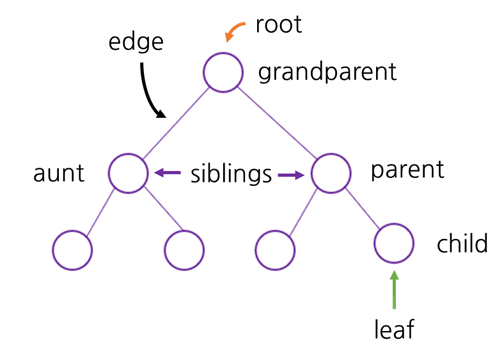
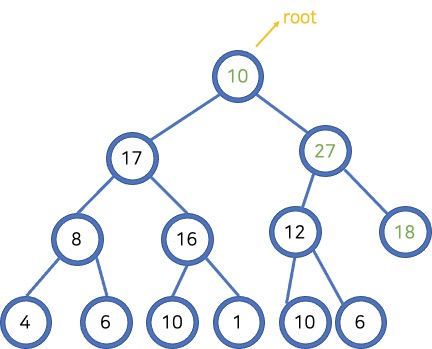
가계도처럼 노드를 나무 형태로 연결한 구조를 트리라고 합니다. 트리에 있는 각각의 요소는 노드입니다. 위 사진에서처럼 노드는 부모, 자식 형태로 이어집니다.
뿌리 (root): 트리의 시작 부분입니다. 뿌리를 통해 들어가서 트리를 탐색합니다. 잎 (leaf): 자식이 딸려있지 않은 부분입니다. 간선 (edge): 두 노드를 연결하는 선입니다. 뿌리로부터의 간선의 수에 따라 level을 나눕니다.
힙
힙은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기반으로 한 자료구조입니다.
힙에는 최대 힙(max heap)과 최소 힙(min heap)이 있습니다. 부모 노드가 자식 노드보다 크면 최대 힙, 반대이면 최소 힙입니다. 가장 큰 숫자가 뿌리에 있게 하려면 최대 힙, 가장 작은 숫자로부터 시작하려면 최소 힙을 사용하면 됩니다.
Heap
-
parent is > children MAX HEAP
-
parent is < children MIN HEAP
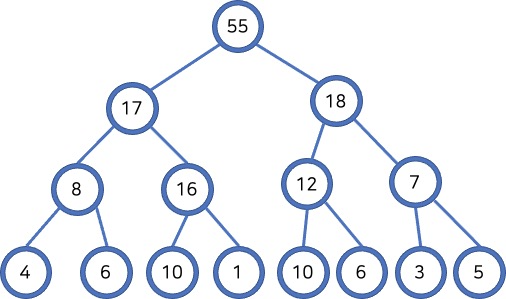
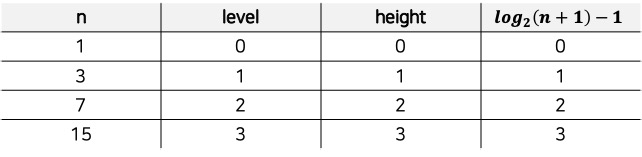
최대 힙에서 노드의 개수 n, level, height, $log_2(n+1) - 1$ 은 위 사진과 같이 나타납니다. $log_2(n+1) - 1$ 은 height와 일치하므로, 트리에 요소가 몇 개 있는지 알면 트리의 높이를 계산할 수 있습니다.
힙: 추가와 제거
힙에 새로운 데이터를 추가하거나 제거할 때 힙의 규칙을 지켜야 합니다. 최대 힙이면 부모 노드가 자식 노드보다 커야 하고 최소 힙은 자식 노드가 부모 노드보다 커야 합니다.
노드 추가
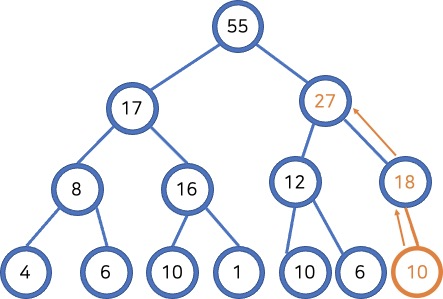
Add:
insert next available space
tricke up
- 비어있는 공간에 노드를 추가합니다.
- 부모 노드보다 큰 숫자인지 확인하고 만약 그렇다면 두 노드를 바꿉니다. (trickle up)
루트 제거
Remove:
remove the root
replace w/ last element
tricle down
- swap with the large of the children
- 루트를 제거합니다.
- 트리의 마지막 요소를 루트에 넣어줍니다.
- 루트에서 시작하여 두 자식 중 큰 노드와 바꿔주어 힙의 규칙을 만족하게 합니다. (trickle down)
무언가를 제거할 때 힙에서는 항상 루트를 제거해야 합니다.
힙: TrickleUp 함수
완전이진트리이기 때문에 노드의 위치는 다음과 같은 성질을 가집니다. children: 2 _ parent + 1 또는 2 _ parent + 2 parent: floor((child-1)/2)
이 성질을 이용하여 노드 추가 과정을 코드로 작성하면 다음과 같습니다.
int lastposition; // 어디까지 요소를 넣었는지 기록
E[] array = (E[]) new Object[size];
public void add(E obj){
array[++lastposition] = obj; // 1. 노드 추가
trickleup(lastposition); // 2. trickle up
}
public void swap(int from, int to){
E tmp = array[from];
array[from] = array[to];
array[to] = tmp;
}
public void trickleup(int position){
if (position == 0)
return;
int parent = (int) Math.floor((position-1)/2)
if (((Comparable<E>) array[position]).compareTo(array.parent)>0) {
swap(position, parent);
trickleup(parent);
}
}
힙: TrickleDown 함수
루트 제거 과정을 코드로 작성하면 다음과 같습니다.
public E remove(){
E tmp = array[0];
swap(0, lastposition--); // 루트와 마지막 노드를 바꿔주고 lastposition을 줄여 배열에서 제거합니다.
trickleDown(0);
return tmp;
}
public void trickleDown(int parent){
int left = 2*parent + 1;
int right = 2*parent + 2;
// 마지막에 왼쪽 자식이 클 때
if (left==lastposition && (((Comparable<E>)array[parent]).compareTo(array[left])<0){
swap(parent, left)
return;
}
// 마지막에 오른쪽 자식이 클 때
if (right==lastposition && (((Comparable<E>)array[parent]).compareTo(array[right])<0){
swap(parent, right)
return;
}
// 마지막에 부모가 클 때
if (left >= lastposition || right >= lastposition)
return;
// 왼쪽 자식이 클 때
if (array[left] > array[right] && array[parent] < array[left]) {
swap(parent, left);
trickleDown(left);
}
// 오른쪽 자식이 클 때
else if (array[parent] < array[right]){
swap(parent, right);
trickleDown(right);
}
}
힙: 정렬
힙 규칙에 맞게 숫자의 순서를 맞추는 과정을 힙 정렬 알고리즘이라고 합니다. 영상에서와 같이, 임의의 숫자들을 나열하고 힙 규칙에 맞게 TrickleDown을 반복하면 그 숫자들이 정렬됩니다.
힙 정렬 알고리즘의 시간 복잡도는 $O(nlogn)$ 입니다. 두 수를 비교해서 하나를 고르는 방식으로 숫자를 골라내기 때문입니다. (총 n개의 숫자를 logn개의 숫자와 비교합니다.)
숫자들의 순서를 바꿔 정렬하기 때문에 데이터의 복사본을 만들 필요가 없다는 점이 힙 정렬의 장점입니다.
트리: 완전 트리와 정 트리
Complete / Full
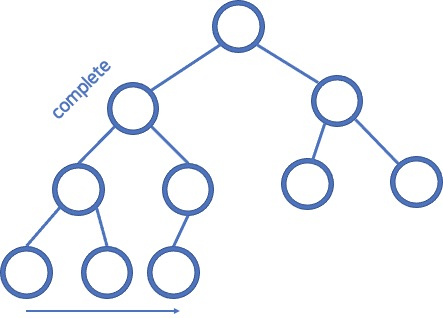
Every non leaf has two children except for the last row & the last row is filled left -> right
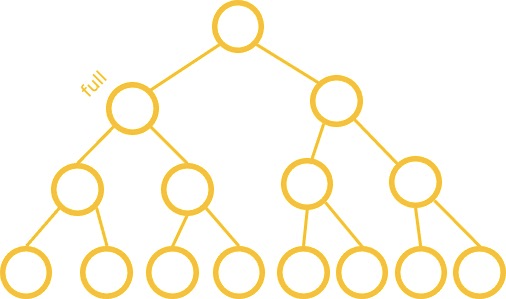
Every non leaf has two children & all the leaves are on the same level
완전 트리 (Complete Tree): 모든 잎이 아닌 노드가 2개의 자식 노드를 가지고 있고 마지막 줄은 왼쪽에서 오른쪽 순서로 채워져 있는 트리입니다.
정 트리 (Full Tree): 모든 잎이 아닌 노드가 2개의 자식 노드를 가지고 있고 모든 잎이 같은 레벨에 있는 트리입니다.
트리: 순회
Trees Traversal
Pre order traversal:
-
visit root node
-
visit left child
-
visit right child
In order traversal:
-
visit left child
-
visit root
-
visit right child
Post order traversal:
-
visit left child
-
visit right child
-
visit root
전위 순회 (Pre order traversal): 루트 노드에서 시작하여 왼쪽 자식 노드에 갔다가 오른쪽 자식 노드로 가는 순회 방법입니다. 다른 모든 노드를 지나기 전에 루트 노드를 방문하기 때문에 이름에 전(Pre)이 들어갑니다.
중위 순회 (In order traversal): 왼쪽 자식 노드에서 시작하여 루트 노드에 갔다가 오른쪽 자식 노드로 가는 순회 방법입니다.
후위 순회 (Post order traversal): 왼쪽 자식 노드에서 시작하여 오른쪽 자식 노드에 갔다가 루트 노드로 가는 순회 방법입니다.
너비 우선 선회/레벨 순서 순회 (Breadth first traversal/level order traversal): 가장 위에 있는 노드에서 시작하여 왼쪽에서 오른쪽으로 가는 순회 방법입니다.
트리: 표현
표현식 트리를 활용하여 굉장히 복잡한 식도 트리 형식으로 표현할 수 있습니다.
예1.
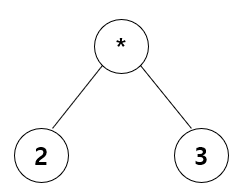
중위 표기식: 2 _ 3 후위 표기식: 2 3 _
예2.
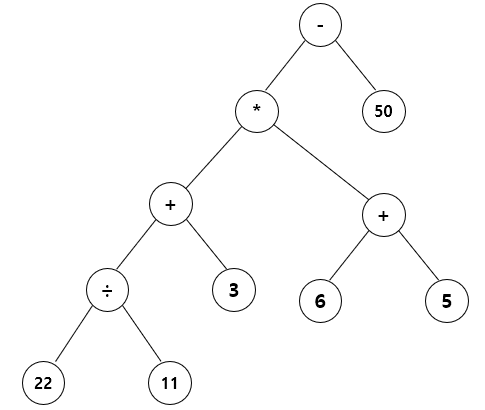
중위 표기식: (((22 / 11) + 3) * (6 + 5)) - 50
후위 표기식: 22 11 / 3 + 6 5 + * 50 -
- 후위 표기식의 장점
https://cho22.tistory.com/33?category=211411
우리가 흔히 쓰는 중위 표기식은 괄호와 연산자 우선순위를 고려해야 하므로, 수식을 왼쪽부터 차례대로 계산할 수 없다. 반면에, 후위 표기식은 괄호 필요 없이 수식을 읽으면서 바로 연산할 수 있기 때문에 컴퓨터가 연산하기 더 편한 방법이다. 예를 들어 a+bc를 후위 표기식으로 바꾸면 abc+가 된다.
- 관련 문제: https://www.acmicpc.net/problem/1918
트리: 노드 클래스
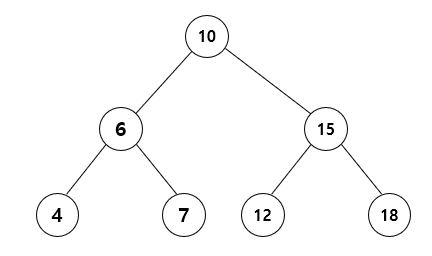
트리에서는 엄마 노드보다 작은 데이터가 왼쪽 자식 노드에 와야 하고 엄마 노드보다 큰 데이터가 오른쪽 자식 노드에 와야 합니다.
그래서 어떤 수를 찾으려고 할 때 엄마 노드보다 작으면 왼쪽으로, 크면 오른쪽으로 이동하게 됩니다. 전체 데이터의 반은 무시하고 logn의 복잡도를 가집니다.
연결 리스트에서 노드가 next 포인터를 갖고 있었던 것처럼, 트리에서는 노드가 left, right 포인터를 갖습니다. 노드 클래스를 코드로 작성하면 다음과 같습니다.
class Node<E> {
E data;
Node <E> left, right;
public Node(E obj){
this.data = obj;
left=right=null;
}
}
트리: 재귀 함수
트리에 새로운 데이터를 추가하는 과정
- 루트에서부터 시작합니다.
- 트리의 규칙에 따라 내려갑니다.
- null인 부분을 찾았다면 그 곳에 새로운 노드를 추가합니다.
이 과정을 코드로 작성하면 다음과 같습니다. 재귀 함수를 이용하여 트리의 규칙에 따라 내려가는 기능을 구현합니다. (함수 시그니처가 비슷한 두 가지 메소드를 만드는 것을 오버로딩이라고 부릅니다.)
public void add (E obj, Node<E> node){
if (((Comparable<E>) obj).compareTo(node.data) > 0){
// go to the right
if(node.right == null) { // 3
node.right = new Node<E>(obj);
return;
}
return add (obj, node.right); // 2
}
// go to the left
if(node.left == null) { // 3
node.left = new Node<E>(obj);
return;
}
return add (obj, node.left); // 2
}
// 트리가 비어있을 경우 (오버로딩)
public void add (E obj){
if (root==null)
root = newNode<E>(obj);
else
add(obj, root);
currentSize++;
}
트리: Contains
이번에는 특정 요소가 트리에 포함되어있는지 확인하는 함수를 구현해보겠습니다. 트리에 새로운 데이터를 추가하는 과정과 비슷하게 동작합니다.
- 루트에서부터 시작합니다.
- 트리의 규칙에 따라 내려갑니다.
- 그 요소를 찾으면 True를 반환하고 null인 노드에 다다르면 False를 반환합니다.
이 과정을 코드로 구현하면 다음과 같습니다. 이번에도 재귀 함수를 이용하여 트리의 규칙에 따라 내려가는 기능을 구현합니다.
public boolean contains (E obj, Node<E> node){
// 트리의 끝에 도달했는데 null
if (node==null)
return false;
// node의 data와 일치
if (((Comparable<E>) obj).compareTo(node.data) == 0)
return true;
// go to the right
if (((Comparable<E>) obj).compareTo(node.data) > 0)
return contains(obj, node.right);
// go to the left
return contains(obj, node.left);
}
트리: 제거
자식 노드의 개수에 따라 트리의 특정 요소를 제거하는 방법은 다음과 같습니다.
-
잎 노드를 제거할 경우 그 노드의 부모 노드의 포인터를 null로 설정하면 됩니다.
-
자식 노드가 하나인 노드를 제거할 경우 그 노드의 부모 노드의 포인터를 자식 노드로 향하게 하면 됩니다. 주의할 점은 부모 노드에서 사용했던 포인터와 같은 포인터(left, right 중 하나)를 사용해야 한다는 것입니다.
-
자식 노드가 2개인 노드를 제거할 경우 중위 후속자와 중위 선임자 중 하나와 자리를 바꾼 후 그 잎 노드를 제거합니다.
중위 후속자(in order successor): 제거하고자 하는 노드에서 시작하여 왼쪽으로 한 번 내려갔다가 계속 오른쪽으로 내려간 곳의 잎 노드입니다. 중위 후속자는 제거하고자 하는 노드보다 작은 노드들 중에서 가장 큰 노드입니다. (중위 순회 방식으로 노드를 탐색할 때 루트 노드를 방문하기 직전에 만나게 되는 노드이기 때문에 중위 후속자라고 부릅니다.)
중위 선임자(in order predessor): 제거하고자 하는 노드에서 시작하여 오른쪽으로 한 번 내려갔다가 계속 왼쪽으로 내려간 곳의 잎 노드입니다. 중위 선임자는 제거하고자 하는 노드보다 큰 노드들 중에서 가장 작은 노드입니다.
트리: 회전 소개
균형 잡힌 트리를 만들기 위해 트리의 노드 위치를 바꾸는 과정을 회전이라고 합니다.
연결 리스트처럼 한 방향으로 나열된 트리는 균형 잡혀 있지 않다고 표현합니다. 균형 잡힌 트리에서는 특정 요소를 탐색하는 시간 복잡도가 O(logn)이지만 균형 잡히지 않은 트리에서는 연결 리스트와 같은 O(n)이 됩니다. 따라서, 데이터를 효율적으로 관리하려면 트리를 균형 있게 만들어야 합니다.
조부모 노드, 부모 노드, 자식 노드의 크기 관계에 따라 우측 회전, 혹은 좌측 회전을 합니다. 트리를 재정렬하면 항상 중간 크기의 요소가 가장 위에 있는 루트가 됩니다.
- 불균형이 왼쪽 서브트리에서 나타날 경우
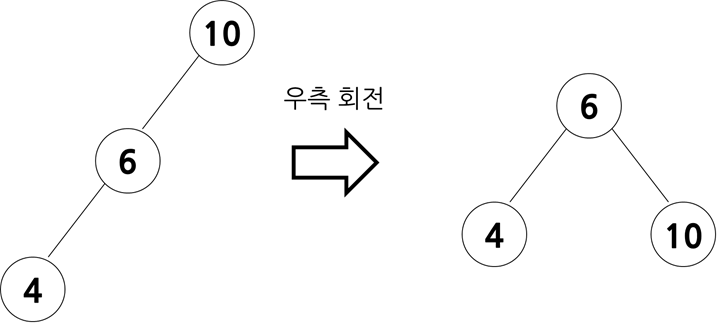
크기 관계는 (조부모 노드) > (부모 노드) > (자식 노드)입니다. 우측 회전을 하여 조부모 노드를 부모 노드의 오른쪽 자식 노드 위치로 옮겨줍니다.
- 불균형이 오른쪽 서브트리에서 나타날 경우
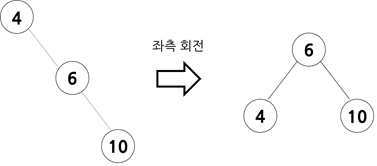
크기 관계는 (조부모 노드) < (부모 노드) < (자식 노드)입니다. 좌측 회전을 하여 조부모 노드를 부모 노드의 왼쪽 자식 노드 위치로 옮겨줍니다.
트리: 회전
지난 번에는 트리가 한 쪽으로 치우친 경우를 살펴보았습니다. 불균형이 왼쪽 서브트리에서 나타나면 우측 회전, 오른쪽 서브트리에서 나타나면 좌측 회전을 하여 이를 해결합니다.
트리가 한 쪽으로 치우치지 않은 경우에는 어떻게 해결할까요? 이럴 경우, 우측 회전과 좌측 회전을 모두 사용하여 불균형을 해소합니다.
- 불균형이 오른쪽 자식의 왼쪽 서브 트리에서 나타날 경우
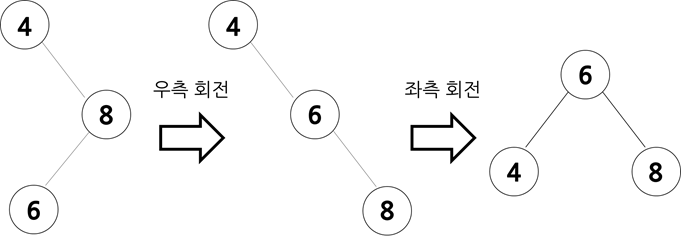
크기 관계는 (부모 노드) > (자식 노드) > (조부모 노드)입니다. 자식 노드에 대해 부모 노드를 우측 회전 후 좌측 회전을 하여 조부모 노드를 부모 노드의 왼쪽 자식 노드 위치로 옮겨줍니다.
- 불균형이 왼쪽 자식의 오른쪽 서브 트리에서 나타날 경우
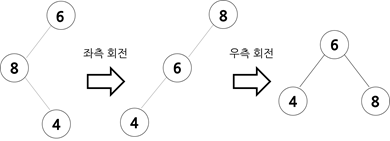
크기 관계는 (부모 노드) > (조부모 노드) > (자식 노드)입니다. 자식 노드에 대해 부모 노드를 좌측 회전 후 우측 회전을 하여 조부모 노드를 부모 노드의 오른쪽 자식 노드 위치로 옮겨줍니다.
트리:회전 (코딩)
다음과 같이 임시 포인터를 사용하여 좌측 회전, 우측 회전을 구현합니다.
// 좌측 회전: 조부모 노드를 부모 노드의 왼쪽 자식 노드 위치로 옮깁니다.
public Node<E> leftRotate (Node<E> node){
Node<E> tmp = node.right; // set temp=grandparents right child
node.right = tmp.left; // set grandparents right child=temp left child
tmp.left = node; // set temp left child=grandparent
return tmp; // use temp instead of grandparent
}
// 우측 회전: 조부모 노드를 부모 노드의 오른쪽 자식 노드 위치로 옮깁니다.
public Node<E> leftRotate (Node<E> node){
Node<E> tmp = node.left;
node.left = tmp.right;
tmp.right = node;
return tmp;
}
트리가 한 쪽으로 치우치지 않을 경우, 우측 회전과 좌측 회전을 둘 다 사용해야 합니다. 위에서 구현한 우측 회전, 좌측 회전 함수를 활용하여 아래와 같이 구현합니다.
// 우측 회전 후 좌측 회전
public Node<E> rightLeftRotate(Node<E> node){
node.right = rightRotate(node.right);
return leftRotate(node);
}
// 좌측 회전 후 우측 회전
public Node<E> leftRightRotate(Node<E> node){
node.left = leftRotate(node.left);
return rightRotate(node);
}


Leave a comment