[Data Structure] Big-Oh notation (빅 오 표기법)
빅 오 표기법
빅 오 표기법은 알고리즘의 효율성을 표시하는 표기법입니다. 빅 오 표기법을 사용하면 어떤 알고리즘을 다른 알고리즘과 비교해서 표현하는 것이 가능합니다.
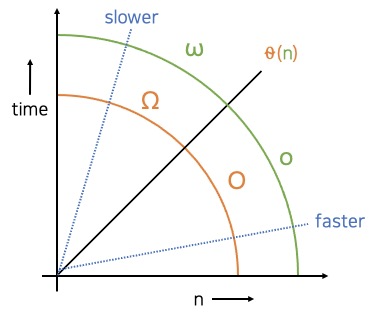
위 그래프는 복잡도가 $n$ 인 알고리즘에 빅 오 표기법을 적용한 결과입니다. $x$축은 복잡도 $n$, $y$축은 필요한 일의 양이나 메모리를 의미합니다.
다른 알고리즘이 이 그래프의 어떤 위치에 있는지에 따라 복잡도 $n$ 인 알고리즘과 다른 알고리즘의 복잡도를 비교할 수 있습니다. 다른 알고리즘이 복잡도 $n$ 인 알고리즘의 아래에 있다면, 같은 일을 하는 데 시간이 덜 들기 때문에 더 빠른 알고리즘이라 합니다. 반대로, 복잡도 $n$ 인 알고리즘의 위에 있다면, 더 느린 알고리즘입니다.
빅 오 표기법에서는 이러한 알고리즘 간의 관계를 다음과 같이 표현합니다.
- $O$ (빅 오 복잡도) : 비교 대상인 그래프가 일치 혹은 아래에 있을 때. 비교 대상인 다른 알고리즘과 같거나 더 빠르다.
- $θ$ (세타 복잡도) : 비교 대상인 그래프가 일치할 때. 비교 대상인 다른 알고리즘과 같다.
- $Ω$ (빅 오메가 복잡도) : 비교 대상인 그래프가 일치 혹은 위에 있을 때. 비교 대상인 다른 알고리즘과 같거나 느리다.
- $o$ (리틀 오 복잡도) : 비교 대상인 그래프가 아래에 있을 때. 비교 대상인 다른 알고리즘보다 더 빠르다.
- $ω$ (리틀 오메가 복잡도) : 비교 대상인 그래프가 위에 있을 때. 비교 대상인 다른 알고리즘과 느리다.
빅 오 표기법 예시
문제
문제 1
$n^{4/3} = O(nlogn)$
힌트) 알고리즘에서는 n이 무한으로 커진 경우를 가정하고 비교한다는 규칙과 log 함수를 포함할 경우 밑은 무시한다는 규칙을 사용하여 풀 수 있습니다.
문제 2
$3n^3 + 4n^2 + 5n + 6 = θ(n^3)$
힌트) 낮은 차수의 항들은 무시한다는 규칙과 모든 상수를 삭제한다는 규칙을 사용하여 풀 수 있습니다.
문제 3
$n(n-1)/2 = O(n^2)$
문제 4
$2^n = w(n)$
문제 5
$n^3 = O(n^2)$
문제 6
$n^2 = O(n^3)$
풀이
문제 1
적당히 큰 수인 1000을 n에 대입하면, 좌변은 10000이고 우변은 $log$의 밑이 10일 때 $O(3000)$입니다. 그래프를 그리면 아래와 같고, 10000은 3000 이하가 아니기 때문에 이 식은 잘못되었습니다.
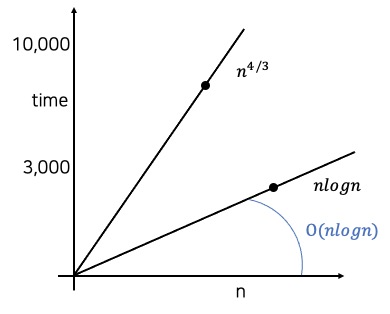
문제 2
낮은 차수의 항들을 무시하면, $3n^3 = θ(n^3)$입니다. 그리고 모든 상수를 삭제하면 $n^3 = θ(n^3)$. 따라서, 이 식은 참입니다.
문제 3
낮은 차수의 항들을 무시하면, $n^2/2 = θ(n^2)$입니다. 그리고 모든 상수를 삭제하면 $n^2 = θ(n^2)$. 따라서, 이 식은 참입니다.
문제 4
적당히 큰 수인 1000을 n에 대입하면, 좌변은 $2^{1000}$이고 우변은 $ω(1000)$입니다. 그래프를 그리면 아래와 같고, 1000은 1000 이상이기 때문에 이 식은 참입니다.
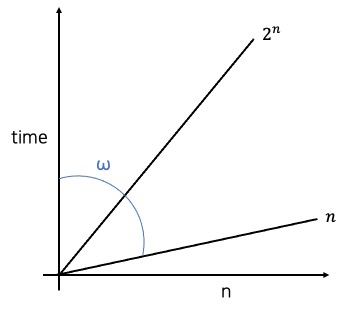
문제 5, 6
$n^2$ 은 $n^3$ 보다 느리게 증가합니다. 따라서, 문제 5는 거짓, 문제 6은 참입니다.
문제 1과 문제 3의 경우, 엄밀하게 풀기 위해서는 로피탈 규칙을 사용해야 합니다. 하지만 본 강의에서는 적당히 큰 수를 대입하는 방법으로도 풀 수 있는 문제들만 다룹니다.


Leave a comment