[Data Structure] AVL Tree (AVL 트리)

AVL 트리

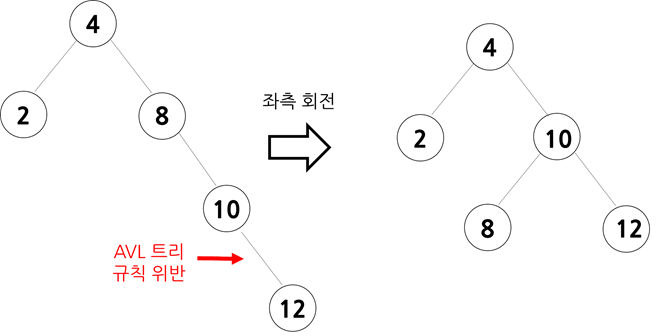
AVL 트리는 스스로 균형을 잡는 이진 탐색 트리입니다. AVL 트리에서는 왼쪽과 오른쪽의 높이 차이가 항상 1보다 작거나 같아야 합니다.

노드

AVL트리의 노드를 만드는 코드는 다음과 같습니다. left, right 노드뿐만 아니라, 기능을 간단하게 구현하기 위한 부모 노드에 대한 포인터도 있습니다.

class Node<T>{
	T data;
	Node<T> left;
	Node<T> right;
	Node<T> parent;
	// 생성자
	public Node(T obj){
		data = obj;
		parent = left = right = null;
}

add 메소드

AVL 트리의 클래스 생성자, add 메소드에 대한 코드입니다. 클래스를 생성 후, 트리가 비어있으면 노드를 추가하고 비어있지 않다면 add 메소드를 재귀로 호출합니다.

// AVL 클래스의 생성자
public AVLTree(){
	root = null;
	currentSize = 0;
}
// add 메소드
public void add(E obj){
	Node<E> node = new Node<E>(obj);
	// 트리가 비어있을 경우
	if (root == null){
		root = node;
		currentSize++;
		return;
	}
	// 트리에 노드가 있을 경우 add 메소드를 재귀로 호출
	add(root, node);
}

재귀 add 메소드

이전의 add 메소드에서 재귀로 호출되는 add 메소드는 다음과 같습니다.

public void add(Node<E> parent, Node<E> new Node){
	// newNode의 data가 parent의 data보다 크면 트리의 오른쪽에 추가하면 됩니다.
	if (((Comparable<E>)newNode.data.compareTo(parent.data)>0{
		if (parent.right == null){
			parent.right = newNode;
			newNode.parent = parent;
			currentSize++;
		}
		else
			add(parent.right, newNode);
	// newNode의 data가 parent의 data보다 작거나 같으면 트리의 왼쪽에 추가하면 됩니다.
	else{
		if (parent.left == null){
			parent.left = newNode;
			newNode.parent = parent;
			currentSize++;
		}
		else
			add(parent.left, newNode);
	// AVL트리가 규칙에 맞게 잘 되어있는지 확인합니다.
	checkBalance(newNode);
}

(참고. add 메소드)

// AVL 클래스의 생성자
public AVLTree(){
	root = null;
	currentSize = 0;
}
// add 메소드
public void add(E obj){
	Node<E> node = new Node<E>(obj);
	// 트리가 비어있을 경우
	if (root == null){
		root = node;
		currentSize++;
		return;
	}
	// 트리에 노드가 있을 경우 add 메소드를 재귀로 호출
	add(root, node);
}

균형 확인 메소드

AVL 트리에서는 왼쪽과 오른쪽의 높이 차이가 항상 1보다 작거나 같아야 합니다. 따라서, 노드를 추가하였을 때 높이의 차이가 1보다 커지면 회전을 하여 트리의 균형을 맞춰주어야 합니다.

트리의 높이 차이를 확인하고 균형을 맞추는 checkBalance 코드는 다음과 같습니다.

public void checkBalance(Node<E> node){
	// 높이 차이가 1 초과 혹은 -1 미만 (AVL 트리 규칙 위반)
	if ((height(node.left) - height(node.right)>1) || (height(node.left) - height(node.right)<-1)){
		rebalance(node);
	// 부모 노드를 계속 확인해서 루트까지 갑니다.
	if (node.parent == null)
		return;
	checkBalance(node.parent);
}

Rebalance 메소드

Rebalance 메소드는 어느 쪽에서 균형이 깨졌는지 확인하고 회전을 하여 균형을 유지합니다.

public void rebalance(Node<E> node){
	// 왼쪽 자식 > 오른쪽 자식
	if (height(node.left) - height(node.right)>1) {
		if(height(node.left.left) > height(node.left.right)) // 왼쪽 서브 트리 > 오른쪽 서브 트리
			node = rightRotate(node); // 우측 회전
		else // 왼쪽 서브 트리 < 오른쪽 서브 트리
			node = leftRightRotate(node); // 좌측-우측 회전
	}
	// 왼쪽 자식 < 오른쪽 자식
	else{
		if(height(node.left.left) > height(node.left.right)) // 왼쪽 서브 트리 > 오른쪽 서브 트리
			node = rightLeftRotate(node); // 우측-좌측 회전
		else // 왼쪽 서브 트리 < 오른쪽 서브 트리
			node = leftRotate(node); // 좌측 회전
	}
	// 루트로 올 때까지 반복합니다.
	if (node.parent == null)
		root=node;
}

adding data 예제

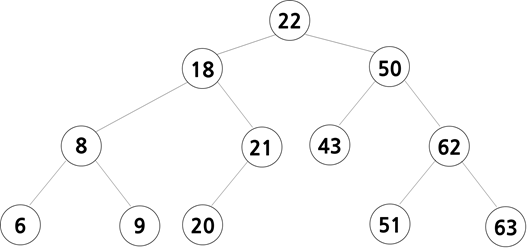
위 사진은 지금까지 만든 add 메소드를 활용하여 43에 18, 22, 9, 21, 6, 8, 20, 63, 50, 62, 51을 순서대로 추가한 결과입니다. 먼저 트리의 규칙에 따라 내려가 잎에 새로운 데이터를 추가합니다. 그리고 균형이 깨졌는지 확인하고 회전을 하여 균형을 유지합니다.

Reference

• BoostCourse